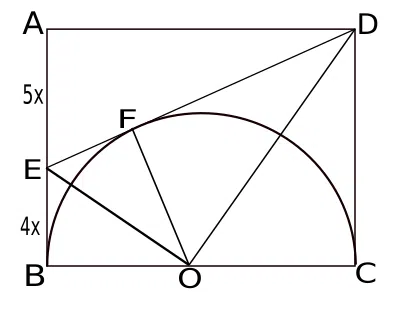
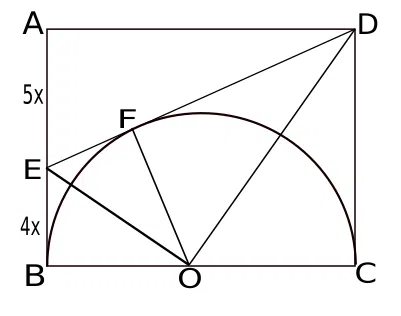
100+ Most Important Geometry Questions for CAT 2025
Geometry is an important topic for the CAT 2025 exam, and doing well in it is crucial for a high score. Geometry questions test your understanding of basic formulas, properties, and theorems, while also helping you improve your problem-solving and spatial skills. We’ve put together over 100+ important geometry questions that cover essential topics like plane geometry, coordinate geometry, solid geometry, and trigonometry, all of which are key for the CAT exam.
This blog is a complete guide to geometry for CAT 2025, offering a range of questions from simple to advanced. You’ll find easy-to-understand explanations to help you grasp the key concepts. Whether you're focusing on triangles, circles, or 3D shapes, practicing these 100+ CAT geometry questions will boost your speed and accuracy, making sure you’re well-prepared for the geometry section in the CAT exam.
Download 100+ CAT Geometry Questions PDF
To make your preparation easier, we’ve compiled 100+ important CAT geometry questions for CAT 2025 in a downloadable PDF. This resource contains key questions from various geometry topics, including plane geometry, coordinate geometry, and solid geometry. It’s perfect for regular practice and revision, helping you to improve both speed and accuracy. Download the PDF today and begin practicing whenever and wherever it’s most convenient for you.
List of 100+ Geometry Questions for CAT 2025
In this section, you'll find a complete list of 100+ geometry questions selected for CAT 2025. The questions range from basic to more difficult ones, giving you a well-rounded preparation. They cover key topics like triangles, circles, quadrilaterals, 3D geometry, coordinate geometry, and trigonometry. Regularly practicing these questions will help you get familiar with the types of questions that appear in the exam and improve your understanding of geometry.
Below, we have listed all 100+ geometry questions along with video solutions to help you understand the concepts better and guide you through solving each problem step by step.
Question 1
Three circles of equal radii touch (but not cross) each other externally. Two other circles, X and Y, are drawn such that both touch (but not cross) each of the three previous circles. If the radius of X is more than that of Y, the ratio of the radii of X and Y is
correct answer:- 1
Question 2
The coordinates of the three vertices of a triangle are: (1, 2), (7, 2), and (1, 10). Then the radius of the incircle of the triangle is
correct answer:- 2
Question 3
The midpoints of sides AB, BC, and AC in ΔABC are M, N, and P, respectively. The medians drawn from A, B, and C intersect the line segments MP, MN and NP at X, Y, and Z, respectively. If the area of ΔABC is 1440 sq cm, then the area, in sq cm, of $$\triangle XYZ$$ is
correct answer:- 90
Question 4
ABCD is a trapezium in which AB is parallel to CD. The sides AD and BC when extended, intersect at point E. If AB = 2 cm, CD = 1 cm, and perimeter of ABCD is 6 cm, then the perimeter, in cm, of $$\triangle AEB$$ is
correct answer:- 1
Question 5
A circular plot of land is divided into two regions by a chord of length $$10\sqrt{3}$$ meters such that the chord subtends an angle of 120° at the center. Then, the area, in square meters, of the smaller region is
correct answer:- 4
Question 6
ABCD is a rectangle with sides AB = 56 cm and BC = 45 cm, and E is the midpoint of side CD. Then, the length, in cm, of radius of incircle of $$\triangle ADE$$ is
correct answer:- 10
Question 7
The surface area of a closed rectangular box, which is inscribed in a sphere, is 846 sq cm, and the sum of the lengths of all its edges is 144 cm. The volume, in cubic cm, of the sphere is
correct answer:- 3
Question 8
A regular octagon ABCDEFGH has sides of length 6 cm each. Then the area, in sq. cm, of the square ACEG is
correct answer:- 4
Question 9
In the figure given below PK: KL = 5:4 and RL: LQ = 2:3, then PM: MQ is
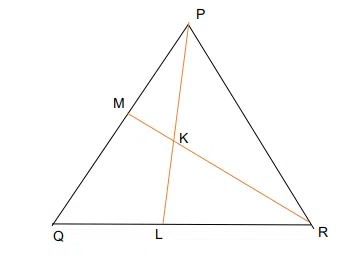
correct answer:- 1
Question 10
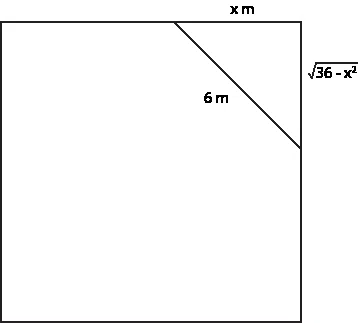
A wedding stage is a square of side 10 metres each. At a corner, a triangular section of the stage is cordoned off using a rope in a straight line. If the length of the rope is 6 metres, what is the maximum area which can be cordoned off in the triangle?
correct answer:- 3
Question 11
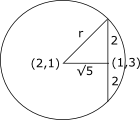
One of the diameters of the circle $$x^2 + y^2 -2x -6y + 6 = 0$$ is a chord of the circle with center (2,1). What is the radius of the circle with center (2,1)?
correct answer:- 1
Question 12
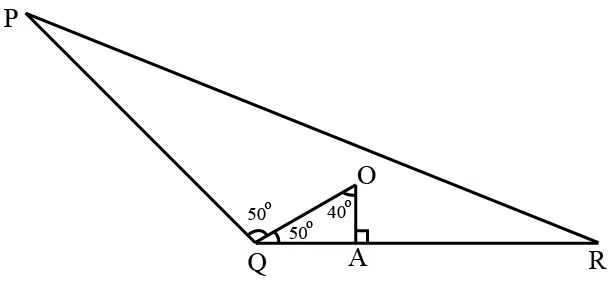
From O, the incentre of $$\triangle$$ PQR, a perpendicular is drawn to the side QR such that it meets QR at A. If $$\angle$$ QOA = $$40^0$$, Then the measure of $$\angle POR$$ is
correct answer:- 2
Question 13
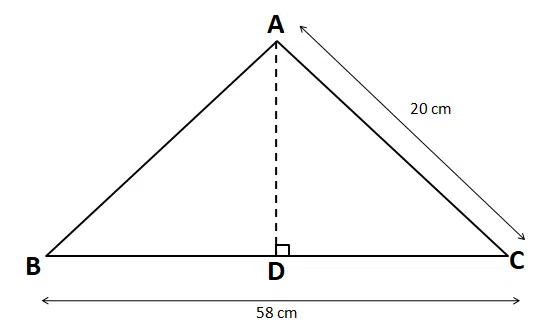
In a triangle, ABC, the length of the longest side is 58 cm. If the area of the triangle is 348 sq. cm and the length of one of the two remaining sides is 20 cm, then find out the length of the third side of the triangle?
correct answer:- 3
Question 14
A semicircle with centre O is drawn inside rectangle ABCD such that the longer side BC is the diameter of the circle. Point E divides AB in the ratio 5:4. Line DE is tangent to the semicircle. If the area of the triangle DEO is 65 square units, then the area (in sq. units) of the rectangle will be
correct answer:- 2
Question 15
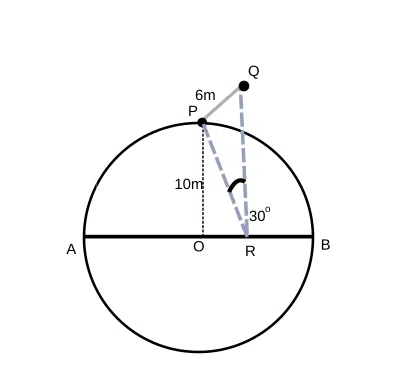
A walking track AB is the diameter of a circular park of radius 10 m. A pole of height 6 m is standing on the circumference of the circular park and it subtends equal angles at A and B. A point R lies on the line AB and the pole subtends 30$$\degree$$ at R. What is the distance of the point R from the center?
correct answer:- 1
Question 16
An equilateral triangle is drawn inside an isosceles right-angled triangle such that both of them share a vertex and the height of both the triangles is the same. If the length of the side of the equilateral triangle is $$a$$, what is the perimeter of the right-angled triangle?
correct answer:- 2
Question 17
Three points lie at a distance of 6 cm from each other. A fourth point, which is not in the same plane as the other 3 points are, is a distance of 8 cm from each of the 3 points. What is the surface area of the packed figure formed by the four points?
correct answer:- 3
Question 18
If the measurements of two sides of a triangle are 34 cm and 42 cm, then the number of possible integral values of the third side is
correct answer:- 3
Question 19
The two circles shown are of radius 5 cm. AB and CD are tangents to them. If AB = 26 cm, what is the length of CD (in cm)?

correct answer:- 24
Question 20
In an obtuse-angled triangle, the difference between the obtuse angle and one of the acute angles is $$24^0$$. The difference between the two acute angles is $$54^0$$. Then which among the following cannot be the sum of the angles taken two at a time?
correct answer:- 1
Question 21
XYWZ is a trapezium with XY parallel to WZ. If XY is 10 cm; XZ is 8 cm, $$\angle XZW$$ is 45 degrees and YW is perpendicular to ZW, find the length of WZ?
correct answer:- 3
Question 22
In given figure parallelogram MNQR has area 74 sq. m. If S is the midpoint of RQ, find the area of NTQ?

correct answer:- 3
Question 23
In the figure given below PQ II RS II TU. If PQ:TU=3:2, then what is the value of SR:TU?
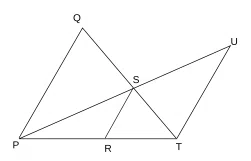
correct answer:- 1
Question 24
Despite x decrease in the length and 2x increase in the breadth of a rectangle, the area remains the same. If the initial ratio of the length and the breadth of the rectangle is 5:4, then find the percentage by which the length of the rectangle is decreased.
For example, enter 20 if the answer is 20%
correct answer:- 60
Question 25
Circles with radius of 6 units and 4 units are drawn in such a way that exactly 3 common tangents are possible. If a direct common tangent from point A touches the circles at points B and C, what is the length of BC?
correct answer:- 3
Question 26
A cone has a radius of 21 cm. 2 cuts parallel to the base are made such that a smaller cone and 2 frustums are formed. The cone and the frustums have the same height. What is the ratio of the lateral surface areas of the smaller frustum and the larger frustum?
correct answer:- 3
Question 27
Balu digs a cylindrical well in his backyard. Just the top surface of the ground (sand) is exposed to the air initially. He heaps the sand excavated in the form of a cone such that the diameter of the well is equal to the diameter of the heap of sand. If the amount of sand exposed to the air has increased by 25% and the diameter of the well is 'n' times the depth of the well, the value of 'n' is
correct answer:- 8
Question 28
x is the hypotenuse of an isosceles right-angled triangle. Taking the base of this isosceles triangle (the smaller side) as the hypotenuse, another isosceles right-angled triangle is drawn. This process is repeated an infinite number of times. What is the ratio of square of the length of the hypotenuse of the original right-angled triangle to the sum of the areas of all the isosceles right-angled triangles?
correct answer:- 4
Question 29
Consider the quadrilateral given below

If it is known that the area of Triangle QOR is 15, SOR is 18 and POS is 12 square units, then find the area of triangle POQ.
correct answer:- 2
Question 30
In a rectangle ABCD, AB = 9 cm and BC = 6 cm. P and Q are two points on BC such that the areas of the figures ABP, APQ, and AQCD are in geometric progression. If the area of the figure AQCD is four times the area of triangle ABP, then BP : PQ : QC is
correct answer:- 3
Question 31
A triangle is drawn with its vertices on the circle C such that one of its sides is a diameter of C and the other two sides have their lengths in the ratio a : b. If the radius of the circle is r, then the area of the triangle is
correct answer:- 2
Question 32
In a regular polygon, any interior angle exceeds the exterior angle by 120 degrees. Then, the number of diagonals of this polygon is
correct answer:- 54
Question 33
A rectangle with the largest possible area is drawn inside a semicircle of radius 2 cm. Then, the ratio of the lengths of the largest to the smallest side of this rectangle is
correct answer:- 1
Question 34
Let $$\triangle ABC$$ be an isosceles triangle such that AB and AC are of equal length. AD is the altitude from A on BC and BE is the altitude from B on AC. If AD and BE intersect at O such that $$\angle AOB = 105^\circ$$, then $$\frac{AD}{BE}$$ equals
correct answer:- 3
Question 35
In a right-angled triangle ∆ABC, the altitude AB is 5 cm, and the base BC is 12 cm. P and Q are two points on BC such that the areas of $$\triangle ABP, \triangle ABQ$$ and $$\triangle ABC$$ are in arithmetic progression. If the area of ∆ABC is 1.5 times the area of $$\triangle ABP$$, the length of PQ, in cm, is
correct answer:- 2
Question 36
A quadrilateral ABCD is inscribed in a circle such that AB : CD = 2 : 1 and BC : AD = 5 : 4. If AC and BD intersect at the point E, then AE : CE equals
correct answer:- 3
Question 37
Let C be the circle $$x^{2} + y^{2} + 4x - 6y - 3 = 0$$ and L be the locus of the point of intersection of a pair of tangents to C with the angle between the two tangents equal to $$60^{\circ}$$. Then, the point at which L touches the line $$x$$ = 6 is
correct answer:- 2
Question 38
In a triangle ABC, AB = AC = 8 cm. A circle drawn with BC as diameter passes through A. Another circle drawn with center at A passes through Band C. Then the area, in sq. cm, of the overlapping region between the two circles is
correct answer:- 3
Question 39
The lengths of all four sides of a quadrilateral are integer valued. If three of its sides are of length 1 cm, 2 cm and 4 cm, then the total number of possible lengths of the fourth side is
correct answer:- 4
Question 40
Suppose the medians BD and CE of a triangle ABC intersect at a point O. If area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is
correct answer:- 9
Question 41
The length of each side of an equilateral triangle ABC is 3 cm. Let D be a point on BC such that the area of triangle ADC is half the area of triangle ABD. Then the length of AD, in cm, is
correct answer:- 3
Question 42
Regular polygons A and B have number of sides in the ratio 1 : 2 and interior angles in the ratio 3 : 4. Then the number of sides of B equals
correct answer:- 10
Question 43
In triangle ABC, altitudes AD and BE are drawn to the corresponding bases. If $$\angle BAC = 45^{\circ}$$ and $$\angle ABC=\theta\ $$, then $$\frac{AD}{BE}$$ equals
correct answer:- 4
Question 44
Let ABCD be a parallelogram such that the coordinates of its three vertices A, B, C are (1, 1), (3, 4) and (−2, 8), respectively. Then, the coordinates of the vertex D are
correct answer:- 4
Question 45
All the vertices of a rectangle lie on a circle of radius R. If the perimeter of the rectangle is P, then the area of the rectangle is
correct answer:- 2
Question 46
A trapezium $$ABCD$$ has side $$AD$$ parallel to $$BC, \angle BAD = 90^\circ, BC = 3$$ cm and $$AD= 8$$ cm. If the perimeter of this trapezium is 36 cm, then its area, in sq. cm, is
correct answer:- 66
Question 47
Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10cm and 20cm, respectively. If the angle $$\angle ADC$$ is equal to $$30^{0}$$ then the area of the parallelogram, in sq.cm is
correct answer:- 2
Question 48
If a triangle ABC, $$\angle BCA=50^{0}$$. D and E are points on $$AB$$ and $$AC$$, respectively, such that $$AD=DE$$. If F is a point on $$BC$$ such that $$BD=DF$$, then $$\angle FDE$$, in degrees, is equal to
correct answer:- 2
Question 49
A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is
correct answer:- 3500
Question 50
The cost of fencing a rectangular plot is ₹ 200 per ft along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is
correct answer:- 1
Question 51
Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is
correct answer:- 30
Question 52
The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is
correct answer:- 1
Question 53
If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is
correct answer:- 1
Question 54
A circle of diameter 8 inches is inscribed in a triangle ABC where $$\angle ABC = 90^\circ$$. If BC = 10 inches then the area of the triangle in square inches is
correct answer:- 120
Question 55
Suppose the length of each side of a regular hexagon ABCDEF is 2 cm.It T is the mid point of CD,then the length of AT, in cm, is
correct answer:- 1
Question 56
If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length, in cm, of each side of the hexagon is
correct answer:- 4
Question 57
From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is
correct answer:- 4
Question 58
Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6cm and is a tangent to C2, then the diameter, in cm, of C1 is
correct answer:- 10
Question 59
The sum of the perimeters of an equilateral triangle and a rectangle is 90cm. The area, T, of the triangle and the area, R, of the rectangle, both in sq cm, satisfying the relationship $$R=T^{2}$$. If the sides of the rectangle are in the ratio 1:3, then the length, in cm, of the longer side of the rectangle, is
correct answer:- 1
Question 60
Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to
correct answer:- 1
Question 61
The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is
correct answer:- 4
Question 62
In a trapezium $$ABCD$$, $$AB$$ is parallel to $$DC$$, $$BC$$ is perpendicular to $$DC$$ and $$\angle BAD=45^{0}$$. If $$DC$$ = 5cm, $$BC$$ = 4 cm,the area of the trapezium in sq cm is
correct answer:- 28
Question 63
The points (2,1) and (-3,-4) are opposite vertices of a parallelogram.If the other two vertices lie on the line $$x+9y+c=0$$, then c is
correct answer:- 4
Question 64
A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
correct answer:- 1
Question 65
On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
correct answer:- 1
Question 66
A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
correct answer:- 1
Question 67
Let T be the triangle formed by the straight line 3x + 5y - 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is
correct answer:- 9
Question 68
If the rectangular faces of a brick have their diagonals in the ratio $$3 : 2 \surd3 : \surd{15}$$, then the ratio of the length of the shortest edge of the brick to that of its longest edge is
correct answer:- 2
Question 69
Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is
correct answer:- 1
Question 70
In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is
correct answer:- 4
Question 71
AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to
correct answer:- 3
Question 72
Let A and B be two regular polygons having a and b sides, respectively. If b = 2a and each interior angle of B is $$\frac{3}{2}$$ times each interior angle of A, then each interior angle, in degrees, of a regular polygon with a + b sides is
correct answer:- 150
Question 73
In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is
correct answer:- 3
Question 74
A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is
correct answer:- 1
Question 75
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
correct answer:- 1
Question 76
The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is
correct answer:- 2
Question 77
Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
correct answer:- 4
Question 78
From a rectangle ABCD of area 768 sq cm, a semicircular part with diameter AB and area 72π sq cm is removed. The perimeter of the leftover portion, in cm, is
correct answer:- 3
Question 79
A triangle ABC has area 32 sq units and its side BC, of length 8 units, lies on the line x = 4. Then the shortest possible distance between A and the point (0,0) is
correct answer:- 2
Question 80
On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is
correct answer:- 24
Question 81
The area of a rectangle and the square of its perimeter are in the ratio 1 ∶ 25. Then the lengths of the shorter and longer sides of the rectangle are in the ratio
correct answer:- 1
Question 82
A chord of length 5 cm subtends an angle of 60° at the centre of a circle. The length, in cm, of a chord that subtends an angle of 120° at the centre of the same circle is
correct answer:- 1
Question 83
A parallelogram ABCD has area 48 sqcm. If the length of CD is 8 cm and that of AD is s cm, then which one of the following is necessarily true?
correct answer:- 2
Question 84
In a circle with center O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
correct answer:- 3
Question 85
In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is
correct answer:- 1
Question 86
A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With $$\pi$$ = 22/7, the volume, in cubic ft, of the remaining part of the cone is
correct answer:- 198
Question 87
Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be
correct answer:- 4
Question 88
Points E, F, G, H lie on the sides AB, BC, CD, and DA, respectively, of a square ABCD. If EFGH is also a square whose area is 62.5% of that of ABCD and CG is longer than EB, then the ratio of length of EB to that of CG is
correct answer:- 4
Question 89
Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?
correct answer:- 1
Question 90
In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is
correct answer:- 1
Question 91
Let P be an interior point of a right-angled isosceles triangle ABC with hypotenuse AB. If the perpendicular distance of P from each of AB,BC,and CA is $$4(\sqrt{2}-1)$$ cm,then the area, in sq cm, of the triangle ABC is
correct answer:- 16
Question 92
If three sides of a rectangular park have a total length 400 ft, then the area of the park is maximum when the length (in ft) of its longer side is
correct answer:- 200
Question 93
ABCD is a quadrilateral inscribed in a circle with centre O such that O lies inside the quadrilateral. If $$\angle COD = 120$$ degrees and $$\angle BAC = 30$$ degrees, then the value of $$\angle BCD$$ (in degrees) is
correct answer:- 90
Question 94
The points (2, 5) and (6, 3) are two end points of a diagonal of a rectangle. If the other diagonal has the equation y =3x+c,then c is
correct answer:- 4
Question 95
The base of a vertical pillar with uniform cross section is a trapezium whose parallel sides are of lengths 10 cm and 20 cm while the other two sides are of equal length. The perpendicular distance between the parallel sides of the trapezium is 12 cm. If the height of the pillar is 20 cm, then the total area, in sq cm, of all six surfaces of the pillar is
correct answer:- 3
Question 96
Let ABCDEF be a regular hexagon with each side of length 1 cm. The area (in sq cm) of a square with AC as one side is
correct answer:- 2
Question 97
The shortest distance of the point $$(\frac{1}{2},1)$$ from the curve y = I x -1I + I x + 1I is
correct answer:- 1
Question 98
Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is
correct answer:- 24
Question 99
A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is $$9\pi$$ cubic centimeters. Then the vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is
correct answer:- 6
Question 100
A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to
correct answer:- 2
Question 101
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is
correct answer:- 2
Question 102
From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is
correct answer:- 2
Question 103
The area of the closed region bounded by the equation I x I + I y I = 2 in the two-dimensional plane is
correct answer:- 3