Sign in
Please select an account to continue using cracku.in
↓ →
The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is
We are given that :
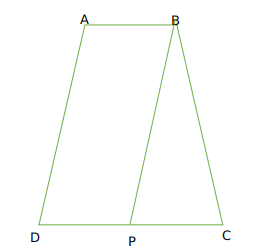
Let DP =x
So AB =x
Now DP=CP
So CD = 2x
Now let height of trapezium be h
we can say A(Parallelogram ABPD ) = xh
And A (BPC) =$$\frac{1}{2}xh$$
Now by condition$$xh-\frac{1}{2}xh=10$$
$$\frac{xh}{2}=10$$
so xh =20
Now therefore area of trapezium ABCD = $$\frac{1}{2}\left(x+2x\right)h\ =\ \frac{3}{2}xh\ =\ 30$$

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation