If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is

All the sides of the rhombus are equal.

The area of a rhombus is $$12\ cm^2$$

Considering d1 to be the length of the longer diagonal, d2 to be the length of the shorter diagonal.

The area of a rhombus is $$\left(\frac{1}{2}\right)\left(d1\right)\cdot\left(d2\right)\ =\ 12$$

d1*d2 = 24.

The length of the side of a rhombus is given by $$\frac{\sqrt{\ d1^2+d2^2}}{2}$$. This is because the two diagonals and a side from a right-angled triangle with sides d1/2, d2/2 and the side length.

$$\frac{\sqrt{\ d1^2+d2^2}}{2}=\ 5$$

Hence $$\sqrt{\ d1^2+d2^2}\ =\ 10$$

$$d1^2+d2^2\ =\ 100$$

Using d1*d2 = 24, 2*d1*d2 = 48.

$$d1^2+d2^2\ +2\cdot d1\cdot d2=\ 100+48\ =\ 148$$

$$d1^2+d2^2\ -2\cdot d1\cdot d2=\ 100-48\ =\ 52$$

$$d1+d2\ =\ \sqrt{\ 148}$$  (1)

d1-d2 = $$\sqrt{52}$$   (2)

(1) + (2)= 2*(d1) = 2*($$\sqrt{\ 37}+\sqrt{\ 13}$$)

d1 = $$\sqrt{\ 37}+\sqrt{\ 13}$$

or 

In a rhombus the area of a Rhombus is given by :

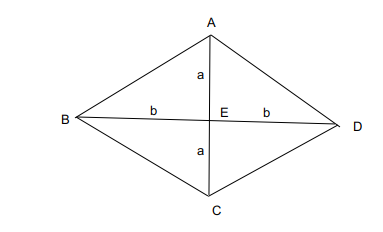
The diagonals perpendicularly bisect each other. Considering the length of the diagonal to be 2a, 2b.

The area of a Rhombus is : $$\left(\frac{1}{2}\right)\cdot\left(2a\right)\cdot\left(2b\right)\ =\ 12$$

ab =6.

The length of each side is : $$\sqrt{\ a^2+b^2}$$ = 5, $$a^2+b^{2\ }=\ 25,\ $$

$$\left(a+b\right)^2=\ 37,\ \left(a+b\right)\ =\ \sqrt{\ 37}$$

($$\left(a-b\right)^2=\ 13,\ a-b\ =\ \sqrt{\ 13}$$

$$2a\ =\ \left(\sqrt{\ 37}+\sqrt{\ 13}\right)$$,  $$2b\ =\ \left(\sqrt{\ 37}-\sqrt{\ 13}\right)$$.

2a is longer diagonal which is equal to $$\ \left(\sqrt{\ 37}+\sqrt{\ 13}\right)$$