Top 54 CAT 2D & 3D LR Questions PDF With Video Solutions
LRDI 2D and 3D LR is one of the important topics in the CAT LRDI section and we have compiled list of all important questions with video solutions. These questions can be a bit challenging, so ensure that you are aware of the Important ways to represent and solve '2D and 3D' Sets in LRDI. You can check out these CAT 2D and 3D LRDI questions from the CAT Previous year papers. This post will look into some important LRDI 2D and 3D LR Questions for CAT. These are a good source of practice for CAT preparation; If you want to practice these questions, you can download these Important 2D and 3D LRDI Questions for CAT (with detailed answers) PDF below, which is completely Free.
Note: No Sign-Up is required to download the PDF
CAT 2D and 3D LR Questions Weightage Over Past 4 Years
Year |
No. Of Questions |
| 2024 | 0 |
| 2023 | 0 |
2022 | 2 |
2021 | 0 |
| 2020 | 1 |
CAT 2024 2D & 3D LR questions
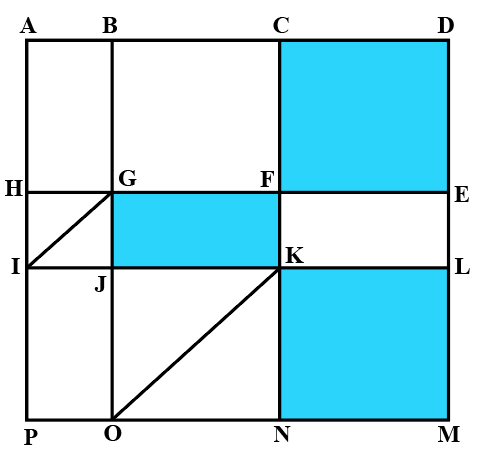
The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles - shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
Question 1
One resident whose house is located at L, needs to visit the post office as well as the bank. What is the minimum distance (in m) he has to walk starting from his residence and returning to his residence after visiting both the post office and the bank?
correct answer:-2
Instruction for set 1:

The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles - shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
Question 2
One person enters the gated area and decides to walk as much as possible before leaving the area without walking along any path more than once and always walking next to one of the lakes. Note that he may cross a point multiple times. How much distance (in m) will he walk within the gated area?
correct answer:-3
Instruction for set 1:

The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles - shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
Question 3
One resident takes a walk within the gated area starting from A and returning to A without going through any point (other than A) more than once. What is the maximum distance (in m) she can walk in this way?
correct answer:-5100
Instruction for set 1:

The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles - shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
Question 4
Visitors coming for morning walks are allowed to enter as long as they do not pass by any of the residences and do not cross any point (except C) more than once. What is the maximum distance (in m) that such a visitor can walk within the gated area?
correct answer:-3500
CAT 2022 2D & 3D LR questions

Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in northsouth direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
Question 1
If Hari is ready to board a train at 8:05 am from station M, then when is the earliest that he can reach station N?
correct answer:-1
Instruction for set 1:

Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in northsouth direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
Question 2
If Priya is ready to board a train at 10:25 am from station T, then when is the earliest that she can reach station S?
correct answer:-1
Instruction for set 1:

Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in northsouth direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
Question 3
Haripriya is expected to reach station S late. What is the latest time by which she must be ready to board at station S if she must reach station B before 1 am via station R?
correct answer:-1
Instruction for set 1:

Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in northsouth direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
Question 4
What is the minimum number of trains that are required to provide the service on the AB line (considering both north and south directions)?
correct answer:-8
Instruction for set 1:

Given above is the schematic map of the metro lines in a city with rectangles denoting terminal stations (e.g. A), diamonds denoting junction stations (e.g. R) and small filled-up circles denoting other stations. Each train runs either in east-west or north-south direction, but not both. All trains stop for 2 minutes at each of the junction stations on the way and for 1 minute at each of the other stations. It takes 2 minutes to reach the next station for trains going in east-west direction and 3 minutes to reach the next station for trains going in northsouth direction. From each terminal station, the first train starts at 6 am; the last trains leave the terminal stations at midnight. Otherwise, during the service hours, there are metro service every 15 minutes in the north-south lines and every 10 minutes in the east-west lines. A train must rest for at least 15 minutes after completing a trip at the terminal station, before it can undertake the next trip in the reverse direction. (All questions are related to this metro service only. Assume that if someone reaches a station exactly at the time a train is supposed to leave, (s)he can catch that train.)
Question 5
What is the minimum number of trains that are required to provide the service in this city?
correct answer:-48
Instruction for set 2:
Every day a widget supplier supplies widgets from the warehouse (W) to four locations - Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
Question 6
If the last location visited is Ahmednagar, then what is the total distance covered in the route (in km)?
correct answer:-35
Instruction for set 2:
Every day a widget supplier supplies widgets from the warehouse (W) to four locations - Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
Question 7
If the total number of widgets delivered in a day is 250 units, then what is the total distance covered in the route (in km)?
correct answer:-38
Instruction for set 2:
Every day a widget supplier supplies widgets from the warehouse (W) to four locations - Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
Question 8
What is the chance that the total number of widgets delivered in a day is 260 units and the route ends at Bikrampore?
correct answer:-4
Instruction for set 2:
Every day a widget supplier supplies widgets from the warehouse (W) to four locations - Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
Question 9
If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?
correct answer:-1
Instruction for set 2:
Every day a widget supplier supplies widgets from the warehouse (W) to four locations - Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
Question 10
If Ahmednagar is not the first location to be visited in a route and the total route distance is 29 km, then which of the following is a possible number of widgets delivered on that day?
correct answer:-1
CAT 2020 2D & 3D LR questions
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters - Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
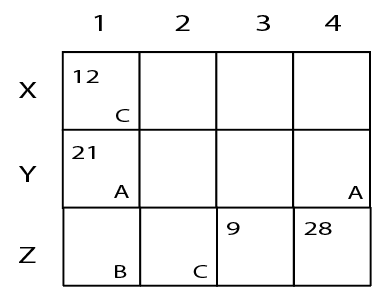
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Question 1
How many mango trees were there in total?
correct answer:-3
Instruction for set 1:
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters - Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:

The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Question 2
Which of the following is the correct sequence of trees received by Abha, Bina, Chitra and Dipti in that order?
correct answer:-1
Instruction for set 1:
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters - Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:

The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Question 3
How many pine trees did Chitra receive?
correct answer:-1
Instruction for set 1:
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters - Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:

The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Question 4
Who got the plot with the smallest number of trees and how many trees did that plot have?
correct answer:-2
Instruction for set 1:
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters - Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:

The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Question 5
Which of the following statements is NOT true?
correct answer:-2
Instruction for set 1:
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters - Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:

The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Question 6
Which column had the highest number of trees?
correct answer:-1


