Please enter the following details
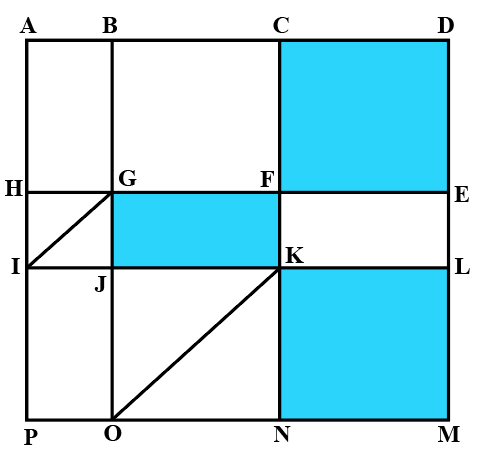
The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles - shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
One resident whose house is located at L, needs to visit the post office as well as the bank. What is the minimum distance (in m) he has to walk starting from his residence and returning to his residence after visiting both the post office and the bank?
The first thing to realise here is the lengths of the paths.
KN should be equal to LM, giving the length of KO using Pythagoras theorem as 500m
Similarly, the length of HJ=OP=150m and length of GJ=EL=200m, giving the length of HG as 250 m
The shortest path from L to B and then to P (or the other way around would involve) using these hypotenuses as much as possible instead of the two adjacent sides. The shortest can be visualised as shown below or multitude of others variations, as there are multiple ways that would make one travel the shortest distance)
The below figure is the simplest one for visualisation.
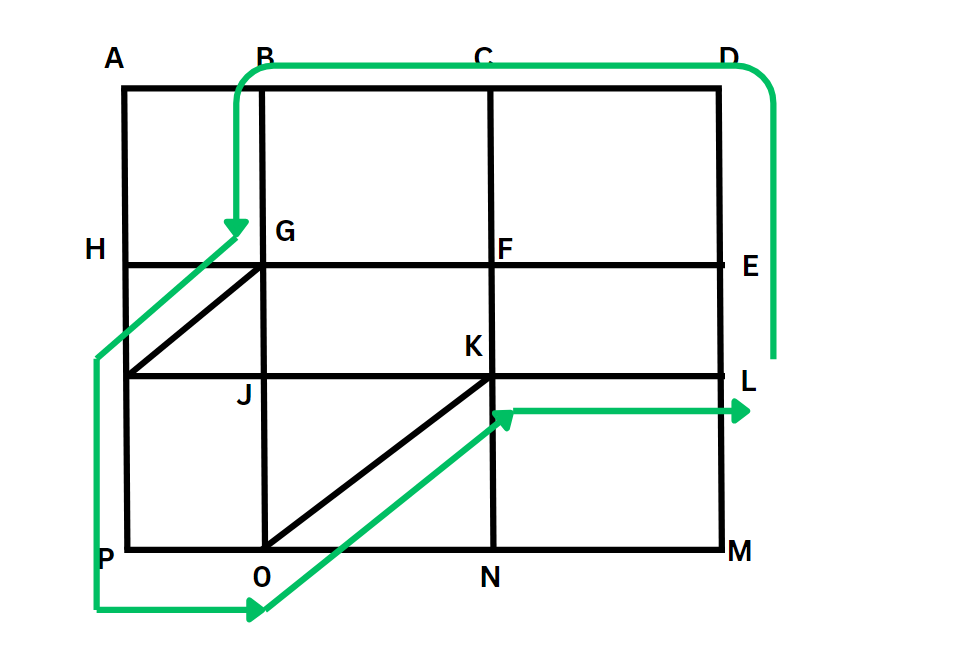
Other possible paths are L-E-F-C-.. and following the same path.
The shortest distance in each of these instance would be LE+ED+DC+CB+BG+GI+IP+PO+OK+KL
Which would be 200+400+300+300+400+250+400+150+500+300 = 3200
Therefore, Option B is the correct answer.
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
