Top 23 CAT Quant Based LR Questions PDF With Video Solutions
Practice Quant Based LR questions for CAT with detailed video solutions. The best way to prepare for these set types is by practicing questions from CAT Previous Papers. Keep solving diverse questions from diverse resources. Also, keep giving numerous mock tests where you get to experience the type and familiarity of Quant Based LR Questions in the actual CAT. These are one of the most and common type of questions that are being asked in the exam every year.
Note: No Sign-Up is required to download the PDF
CAT Quant Based LR Questions Weightage Over Past 4 Years
Year |
No. Of Questions |
| 2024 | 0 |
| 2023 | 3 |
2022 | 1 |
2021 | 0 |
| 2020 | 0 |
CAT 2025 Quant Based LR questions
The following charts depict details of research papers written by four authors, Arman, Brajen, Chintan, and Devon. The papers were of four types, single-author, two-author, three-author, and four-author, that is, written by one, two, three, or all four of these authors, respectively. No other authors were involved in writing these papers.
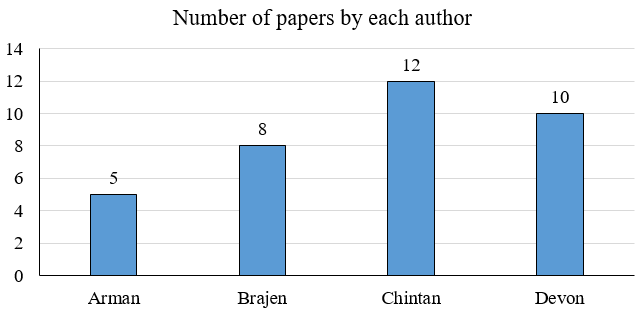
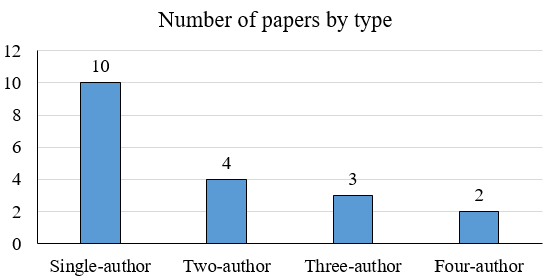
The following additional facts are known.
1. Each of the authors wrote at least one of each of the four types of papers.
2. The four authors wrote different numbers of single-author papers.
3. Both Chintan and Devon wrote more three-author papers than Brajen.
4. The number of single-author and two-author papers written by Brajen were the same.
Question 1
What was the total number of two-author and three-author papers written by Brajen?
correct answer:-4
Instruction for set 1:
The following charts depict details of research papers written by four authors, Arman, Brajen, Chintan, and Devon. The papers were of four types, single-author, two-author, three-author, and four-author, that is, written by one, two, three, or all four of these authors, respectively. No other authors were involved in writing these papers.


The following additional facts are known.
1. Each of the authors wrote at least one of each of the four types of papers.
2. The four authors wrote different numbers of single-author papers.
3. Both Chintan and Devon wrote more three-author papers than Brajen.
4. The number of single-author and two-author papers written by Brajen were the same.
Question 2
Which of the following statements is/are NECESSARILY true?
i. Chintan wrote exactly three two-author papers.
ii. Chintan wrote more single-author papers than Devon.
correct answer:-1
Instruction for set 1:
The following charts depict details of research papers written by four authors, Arman, Brajen, Chintan, and Devon. The papers were of four types, single-author, two-author, three-author, and four-author, that is, written by one, two, three, or all four of these authors, respectively. No other authors were involved in writing these papers.


The following additional facts are known.
1. Each of the authors wrote at least one of each of the four types of papers.
2. The four authors wrote different numbers of single-author papers.
3. Both Chintan and Devon wrote more three-author papers than Brajen.
4. The number of single-author and two-author papers written by Brajen were the same.
Question 3
Which of the following statements is/are NECESSARILY true?
i. Arman wrote three-author papers only with Chintan and Devon.
ii. Brajen wrote three-author papers only with Chintan and Devon.
correct answer:-2
Instruction for set 1:
The following charts depict details of research papers written by four authors, Arman, Brajen, Chintan, and Devon. The papers were of four types, single-author, two-author, three-author, and four-author, that is, written by one, two, three, or all four of these authors, respectively. No other authors were involved in writing these papers.


The following additional facts are known.
1. Each of the authors wrote at least one of each of the four types of papers.
2. The four authors wrote different numbers of single-author papers.
3. Both Chintan and Devon wrote more three-author papers than Brajen.
4. The number of single-author and two-author papers written by Brajen were the same.
Question 4
If Devon wrote more than one two-author papers, then how many two-author papers did Chintan write?
correct answer:-3
Instruction for set 2:
A train travels from Station A to Station E, passing through stations B, C, and D, in that order. The train has a seating capacity of 200. A ticket may be booked from any station to any other station ahead on the route, but not to any earlier station.
A ticket from one station to another reserves one seat on every intermediate segment of the route. For example, a ticket from B to E reserves a seat in the intermediate segments B - C, C - D, and D - E.
The occupancy factor for a segment is the total number of seats reserved in the segment as a percentage of the seating capacity. The total number of seats reserved for any segment cannot exceed 200.
The following information is known.
1. Segment C - D had an occupancy factor of 95%. Only segment B - C had a higher occupancy factor.
2. Exactly 40 tickets were booked from B to C and 30 tickets were booked from B to E.
3. Among the seats reserved on segment D - E, exactly four-sevenths were from stations before C.
4. The number of tickets booked from A to C was equal to that booked from A to E, and it was higher than that from B to E.
5. No tickets were booked from A to B, from B to D and from D to E.
6. The number of tickets booked for any segment was a multiple of 10.
Question 5
What was the occupancy factor for segment D - E?
correct answer:-2
Instruction for set 2:
A train travels from Station A to Station E, passing through stations B, C, and D, in that order. The train has a seating capacity of 200. A ticket may be booked from any station to any other station ahead on the route, but not to any earlier station.
A ticket from one station to another reserves one seat on every intermediate segment of the route. For example, a ticket from B to E reserves a seat in the intermediate segments B - C, C - D, and D - E.
The occupancy factor for a segment is the total number of seats reserved in the segment as a percentage of the seating capacity. The total number of seats reserved for any segment cannot exceed 200.
The following information is known.
1. Segment C - D had an occupancy factor of 95%. Only segment B - C had a higher occupancy factor.
2. Exactly 40 tickets were booked from B to C and 30 tickets were booked from B to E.
3. Among the seats reserved on segment D - E, exactly four-sevenths were from stations before C.
4. The number of tickets booked from A to C was equal to that booked from A to E, and it was higher than that from B to E.
5. No tickets were booked from A to B, from B to D and from D to E.
6. The number of tickets booked for any segment was a multiple of 10.
Question 6
How many tickets were booked from Station A to Station E?
correct answer:-50
Instruction for set 2:
A train travels from Station A to Station E, passing through stations B, C, and D, in that order. The train has a seating capacity of 200. A ticket may be booked from any station to any other station ahead on the route, but not to any earlier station.
A ticket from one station to another reserves one seat on every intermediate segment of the route. For example, a ticket from B to E reserves a seat in the intermediate segments B - C, C - D, and D - E.
The occupancy factor for a segment is the total number of seats reserved in the segment as a percentage of the seating capacity. The total number of seats reserved for any segment cannot exceed 200.
The following information is known.
1. Segment C - D had an occupancy factor of 95%. Only segment B - C had a higher occupancy factor.
2. Exactly 40 tickets were booked from B to C and 30 tickets were booked from B to E.
3. Among the seats reserved on segment D - E, exactly four-sevenths were from stations before C.
4. The number of tickets booked from A to C was equal to that booked from A to E, and it was higher than that from B to E.
5. No tickets were booked from A to B, from B to D and from D to E.
6. The number of tickets booked for any segment was a multiple of 10.
Question 7
How many tickets were booked from Station C?
correct answer:-80
Instruction for set 2:
A train travels from Station A to Station E, passing through stations B, C, and D, in that order. The train has a seating capacity of 200. A ticket may be booked from any station to any other station ahead on the route, but not to any earlier station.
A ticket from one station to another reserves one seat on every intermediate segment of the route. For example, a ticket from B to E reserves a seat in the intermediate segments B - C, C - D, and D - E.
The occupancy factor for a segment is the total number of seats reserved in the segment as a percentage of the seating capacity. The total number of seats reserved for any segment cannot exceed 200.
The following information is known.
1. Segment C - D had an occupancy factor of 95%. Only segment B - C had a higher occupancy factor.
2. Exactly 40 tickets were booked from B to C and 30 tickets were booked from B to E.
3. Among the seats reserved on segment D - E, exactly four-sevenths were from stations before C.
4. The number of tickets booked from A to C was equal to that booked from A to E, and it was higher than that from B to E.
5. No tickets were booked from A to B, from B to D and from D to E.
6. The number of tickets booked for any segment was a multiple of 10.
Question 8
What is the difference between the number of tickets booked to Station C and the number of tickets booked to Station D?
correct answer:-40
Instruction for set 2:
A train travels from Station A to Station E, passing through stations B, C, and D, in that order. The train has a seating capacity of 200. A ticket may be booked from any station to any other station ahead on the route, but not to any earlier station.
A ticket from one station to another reserves one seat on every intermediate segment of the route. For example, a ticket from B to E reserves a seat in the intermediate segments B - C, C - D, and D - E.
The occupancy factor for a segment is the total number of seats reserved in the segment as a percentage of the seating capacity. The total number of seats reserved for any segment cannot exceed 200.
The following information is known.
1. Segment C - D had an occupancy factor of 95%. Only segment B - C had a higher occupancy factor.
2. Exactly 40 tickets were booked from B to C and 30 tickets were booked from B to E.
3. Among the seats reserved on segment D - E, exactly four-sevenths were from stations before C.
4. The number of tickets booked from A to C was equal to that booked from A to E, and it was higher than that from B to E.
5. No tickets were booked from A to B, from B to D and from D to E.
6. The number of tickets booked for any segment was a multiple of 10.
Question 9
How many tickets were booked to travel in exactly one segment?
correct answer:-60
Instruction for set 3:
Aurevia, Brelosia, Cyrenia and Zerathania are four countries with their currencies being Aurels, Brins, Crowns, and Zentars, respectively. The currencies have different exchange values. Crown's currency exchange rate with Zentars = 0.5, i.e., 1 Crown is worth 0.5 Zentars.
Three travelers, Jano, Kira, and Lian set out from Zerathania visiting exactly two of the countries. Each country is visited by exactly two travelers. Each traveler has a unique Flight Cost, which represents the total cost of airfare in traveling to both the countries and back to Zerathania. The Flight Cost of Jano was 4000 Zentars, while that of the other two travelers were 5000 and 6000 Zentars, not necessarily in that order. When visiting a country, a traveler spent either 1000, 2000 or 3000 in the country's local currency. Each traveler had different spends (in the country's local currency) in the two countries he/she visited. Across all the visits, there were exactly two spends of 1000 and exactly one spend of 3000 (in the country's local currency).
The total “Travel Cost” for a traveler is the sum of his/her Flight Cost and the money spent in the countries visited.
The citizens of the four countries with knowledge of these travels made a few observations, with spends measured in their respective local currencies:
i. Aurevia citizen: Jano and Kira visited our country, and their Travel Costs were 3500 and 8000, respectively.
ii. Brelosia citizen: Kira and Lian visited our country, spending 2000 and 3000, respectively. Kira's Travel Cost was 4000.
iii. Cyrenia citizen: Lian visited our country and her Travel Cost was 36000.
Question 10
What is the sum of Travel Costs for all travelers in Zentars?
correct answer:-41000
Instruction for set 3:
Aurevia, Brelosia, Cyrenia and Zerathania are four countries with their currencies being Aurels, Brins, Crowns, and Zentars, respectively. The currencies have different exchange values. Crown's currency exchange rate with Zentars = 0.5, i.e., 1 Crown is worth 0.5 Zentars.
Three travelers, Jano, Kira, and Lian set out from Zerathania visiting exactly two of the countries. Each country is visited by exactly two travelers. Each traveler has a unique Flight Cost, which represents the total cost of airfare in traveling to both the countries and back to Zerathania. The Flight Cost of Jano was 4000 Zentars, while that of the other two travelers were 5000 and 6000 Zentars, not necessarily in that order. When visiting a country, a traveler spent either 1000, 2000 or 3000 in the country's local currency. Each traveler had different spends (in the country's local currency) in the two countries he/she visited. Across all the visits, there were exactly two spends of 1000 and exactly one spend of 3000 (in the country's local currency).
The total “Travel Cost” for a traveler is the sum of his/her Flight Cost and the money spent in the countries visited.
The citizens of the four countries with knowledge of these travels made a few observations, with spends measured in their respective local currencies:
i. Aurevia citizen: Jano and Kira visited our country, and their Travel Costs were 3500 and 8000, respectively.
ii. Brelosia citizen: Kira and Lian visited our country, spending 2000 and 3000, respectively. Kira's Travel Cost was 4000.
iii. Cyrenia citizen: Lian visited our country and her Travel Cost was 36000.
Question 11
How many Zentars did Lian spend in the two countries he visited?
correct answer:-13000
Instruction for set 3:
Aurevia, Brelosia, Cyrenia and Zerathania are four countries with their currencies being Aurels, Brins, Crowns, and Zentars, respectively. The currencies have different exchange values. Crown's currency exchange rate with Zentars = 0.5, i.e., 1 Crown is worth 0.5 Zentars.
Three travelers, Jano, Kira, and Lian set out from Zerathania visiting exactly two of the countries. Each country is visited by exactly two travelers. Each traveler has a unique Flight Cost, which represents the total cost of airfare in traveling to both the countries and back to Zerathania. The Flight Cost of Jano was 4000 Zentars, while that of the other two travelers were 5000 and 6000 Zentars, not necessarily in that order. When visiting a country, a traveler spent either 1000, 2000 or 3000 in the country's local currency. Each traveler had different spends (in the country's local currency) in the two countries he/she visited. Across all the visits, there were exactly two spends of 1000 and exactly one spend of 3000 (in the country's local currency).
The total “Travel Cost” for a traveler is the sum of his/her Flight Cost and the money spent in the countries visited.
The citizens of the four countries with knowledge of these travels made a few observations, with spends measured in their respective local currencies:
i. Aurevia citizen: Jano and Kira visited our country, and their Travel Costs were 3500 and 8000, respectively.
ii. Brelosia citizen: Kira and Lian visited our country, spending 2000 and 3000, respectively. Kira's Travel Cost was 4000.
iii. Cyrenia citizen: Lian visited our country and her Travel Cost was 36000.
Question 12
What was Jano's total spend in the two countries he visited, in Aurels?
correct answer:-1500
Instruction for set 3:
Aurevia, Brelosia, Cyrenia and Zerathania are four countries with their currencies being Aurels, Brins, Crowns, and Zentars, respectively. The currencies have different exchange values. Crown's currency exchange rate with Zentars = 0.5, i.e., 1 Crown is worth 0.5 Zentars.
Three travelers, Jano, Kira, and Lian set out from Zerathania visiting exactly two of the countries. Each country is visited by exactly two travelers. Each traveler has a unique Flight Cost, which represents the total cost of airfare in traveling to both the countries and back to Zerathania. The Flight Cost of Jano was 4000 Zentars, while that of the other two travelers were 5000 and 6000 Zentars, not necessarily in that order. When visiting a country, a traveler spent either 1000, 2000 or 3000 in the country's local currency. Each traveler had different spends (in the country's local currency) in the two countries he/she visited. Across all the visits, there were exactly two spends of 1000 and exactly one spend of 3000 (in the country's local currency).
The total “Travel Cost” for a traveler is the sum of his/her Flight Cost and the money spent in the countries visited.
The citizens of the four countries with knowledge of these travels made a few observations, with spends measured in their respective local currencies:
i. Aurevia citizen: Jano and Kira visited our country, and their Travel Costs were 3500 and 8000, respectively.
ii. Brelosia citizen: Kira and Lian visited our country, spending 2000 and 3000, respectively. Kira's Travel Cost was 4000.
iii. Cyrenia citizen: Lian visited our country and her Travel Cost was 36000.
Question 13
One Brin is equivalent to how many Crowns?
correct answer:-1
Instruction for set 3:
Aurevia, Brelosia, Cyrenia and Zerathania are four countries with their currencies being Aurels, Brins, Crowns, and Zentars, respectively. The currencies have different exchange values. Crown's currency exchange rate with Zentars = 0.5, i.e., 1 Crown is worth 0.5 Zentars.
Three travelers, Jano, Kira, and Lian set out from Zerathania visiting exactly two of the countries. Each country is visited by exactly two travelers. Each traveler has a unique Flight Cost, which represents the total cost of airfare in traveling to both the countries and back to Zerathania. The Flight Cost of Jano was 4000 Zentars, while that of the other two travelers were 5000 and 6000 Zentars, not necessarily in that order. When visiting a country, a traveler spent either 1000, 2000 or 3000 in the country's local currency. Each traveler had different spends (in the country's local currency) in the two countries he/she visited. Across all the visits, there were exactly two spends of 1000 and exactly one spend of 3000 (in the country's local currency).
The total “Travel Cost” for a traveler is the sum of his/her Flight Cost and the money spent in the countries visited.
The citizens of the four countries with knowledge of these travels made a few observations, with spends measured in their respective local currencies:
i. Aurevia citizen: Jano and Kira visited our country, and their Travel Costs were 3500 and 8000, respectively.
ii. Brelosia citizen: Kira and Lian visited our country, spending 2000 and 3000, respectively. Kira's Travel Cost was 4000.
iii. Cyrenia citizen: Lian visited our country and her Travel Cost was 36000.
Question 14
Which of the following statements is NOT true about money spent in the local currency?
correct answer:-1
CAT 2023 Quant Based LR questions
An air conditioner (AC) company has four dealers - D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs - Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known:
1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs.
3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.
4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.
5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.
6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
Question 1
How many Split Inverter ACs did D2 sell?
correct answer:-14
Instruction for set 1:
An air conditioner (AC) company has four dealers - D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs - Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known:
1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs.
3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.
4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.
5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.
6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
Question 2
Which of the following statements is necessarily false?
correct answer:-4
Instruction for set 1:
An air conditioner (AC) company has four dealers - D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs - Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known:
1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs.
3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.
4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.
5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.
6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
Question 3
If D3 and D4 sold an equal number of ACs, then what was the number of Non-inverter ACs sold by D2?
correct answer:-2
Instruction for set 2:
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Question 4
What is the total number of coins in all the boxes in the $$3^{rd}$$ row?
correct answer:-4
Instruction for set 2:
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Question 5
How many boxes have at least one sack containing 9 coins?
correct answer:-3
Instruction for set 2:
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Question 6
For how many boxes are the average and median of the numbers of coins contained in the three sacks in that box the same?
correct answer:-4


