Sign in
Please select an account to continue using cracku.in
↓ →
A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With $$\pi$$ = 22/7, the volume, in cubic ft, of the remaining part of the cone is
Correct Answer: 198
We are given that diameter of base = 8 ft. Therefore, the radius of circular base = 8/2 = 4 ft
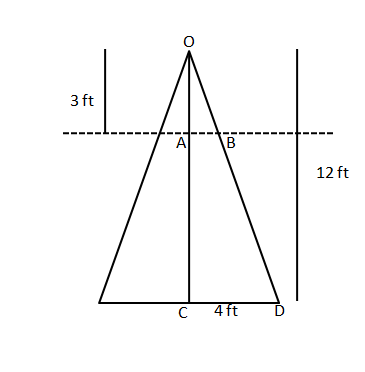
In triangle OAB and OCD
$$\dfrac{OA}{AB} = \dfrac{OC}{CD}$$
$$\Rightarrow$$ AB = $$\dfrac{3*4}{12}$$ = 1 ft.
Therefore, the volume of remaining part = Volume of entire cone - Volume of smaller cone
$$\Rightarrow$$ $$\dfrac{1}{3}*\pi*4^2*12-\dfrac{1}{3}*\pi*1^2*3$$
$$\Rightarrow$$ $$\dfrac{1}{3}*\pi*189$$
$$\Rightarrow$$ $$\dfrac{22}{7*3}*189$$
$$\Rightarrow$$ $$198$$ cubic ft

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation