Function Questions For CAT 2025
Function questions are a frequent topic in the CAT Quant section. They test your understanding of how functions work, domains, ranges, composite functions, inverses, and transformations. In CAT 2025, you can expect both straightforward and tricky function problems. Below are some of the most important types of function questions you should practise to become comfortable with them.
Important Formulas for CAT Function Questions
To solve function questions easily in CAT, you should remember the key formulas and rules related to functions. These formulas help you work with domains, ranges, composite functions, inverses, and transformations quickly. They save time, reduce mistakes, and make even tricky function problems easier to handle. With regular practice, you’ll improve both your speed and accuracy in this topic.
Download CAT Functions Formula PDF
| Concept | Formula / Rule | Explanation / Use |
|---|---|---|
| Basic (Linear) Function | f(x) = ax + b | Straight-line graph; slope a, intercept b |
| Quadratic Function | f(x) = ax2 + bx + c Vertex: x = -b / (2a) |
Parabolic curve; opens up or down |
| Cubic Function | f(x) = ax3 + bx2 + cx + d | S-shaped (sigmoidal) curve |
| Rational Function | f(x) = (ax + b) / (cx + d) | May have vertical/horizontal asymptotes |
| Composite Function | f(g(x)) | Apply g(x) first, then f(x) |
| Inverse Function | f(f−1(x)) = x and f−1(f(x)) = x | Inverse reverses the function |
| Domain Rule | Denominator ≠ 0, √expression ≥ 0 | Determines valid input values |
| Range Rule | Find from domain or use inverse | Describes possible output values |
| Even Function | f(−x) = f(x) | Symmetric about y-axis |
| Odd Function | f(−x) = −f(x) | Symmetric about origin |
| Horizontal Shift | f(x + c) | Shifts graph left by c units |
| Vertical Shift | f(x) + c | Shifts graph up by c units |
| Stretch / Shrink | f(cx) → horizontal c·f(x) → vertical |
Stretches or compresses the graph |
| Piecewise Function | Defined by different rules for intervals | Function depends on input range |
| Absolute Value Function | f(x) = |x| | Output is always non-negative |
| Greatest Integer Function | f(x) = ⌊x⌋ | Rounds x down to nearest integer |
| Signum Function | f(x) = { 1 if x > 0, 0 if x = 0, −1 if x < 0 } | Indicates the sign of the input |
Common Mistakes to Avoid in CAT Function Questions
While solving function problems, students often make avoidable mistakes. Here are some common ones to watch for:
-
Assuming the type wrongly: A function may look linear but has hidden domain restrictions.
-
Mixing up domain & range: Always check valid xxx values first before jumping to outputs.
-
Neglecting composite order: In f(g(x))f(g(x))f(g(x)), you must compute g(x)g(x)g(x) first, then apply fff.
-
Wrong inverse operations: Mistakes in algebra when finding f−1(x)f^{-1}(x)f−1(x) are frequent.
-
Overlooking piecewise parts: If a function is defined piecewise, ensure you're using the correct piece for the input.
-
Ignoring transformation impact: For f(x+c)f(x + c)f(x+c) or f(cx)f(cx)f(cx), wrong shifts or stretches often lead to errors.
List of CAT Function Questions
Question 1
Let $$f(x) = ax^2 + bx + c$$, where a, b and c are certain constants and $$a \neq 0$$ ?
It is known that $$f(5) = - 3f(2)$$. and that 3 is a root of $$f(x) = 0$$.
What is the other root of f(x) = 0?
correct answer:- 2
Question 2
The area of the region satisfying the inequalities $$\mid x\mid-y\leq1,y\geq0$$ and $$y\leq1$$ is
correct answer:- 3
Question 3
Let g(x) be a function such that g(x+1) + g(x-1) = g(x) for every real x. Then for what value of p is the relation g(x+p) = g(x) necessarily true for every real x?
correct answer:- 4
DIRECTIONS for the following questions: These questions are based on the situation given below: In each of the questions a pair of graphs F(x) and F1(x) is given. These are composed of straight-line segments, shown as solid lines, in the domain $$x\epsilon (-2, 2)$$.
choose the answer as
a. If F1(x) = - F(x)
b. if F1(x) = F(- x)
c. if F1(x) = - F(- x)
d. if none of the above is true
Question 4
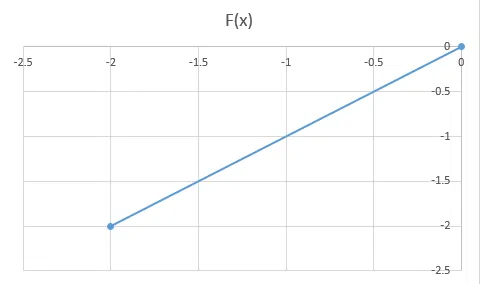
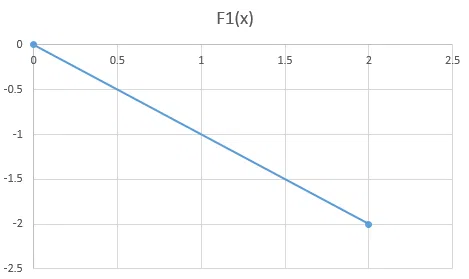
correct answer:- 2
Question 5
Suppose for any real number x, [x] denotes the greatest integer less than or equal to x. Let L(x, y) = [x] + [y] + [x + y] and R(x, y) = [2x] + [2y]. Then it is impossible to find any two positive real numbers x and y for which
correct answer:- 4
Question 6
Let $$f(x) = ax^2 + bx + c$$, where a, b and c are certain constants and $$a \neq 0$$ ?
It is known that f(5) = - 3f(2). and that 3 is a root of f(x) = 0.
What is the value of a + b + c?
correct answer:- 5






























