From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is

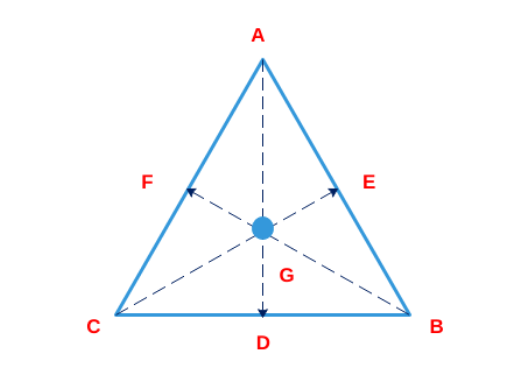
Based on the question: AD, CE and BF are the three altitudes of the triangle. It has been stated that {GD+GE+GF = s}

Now since the triangle is equilateral, let the length of each side be "a". So area of triangle will be

$$\frac{1}{2}\times\ GD\times\ a+\ \frac{1}{2}\times\ GE\times\ a\ +\frac{1}{2}\times\ GF\times\ a=\frac{\sqrt{\ 3}}{4}a^2$$

Now $$GD+GE+GF=\frac{\sqrt{\ 3}a}{2}$$ or $$s=\frac{\sqrt{\ 3}a}{2}\ or\ a=\frac{2s}{\sqrt{\ 3}}$$

Given the area of the equilateral triangle = $$\ \frac{\sqrt{3}}{4}a^2\ $$ ; substituting the value of 'a' from above, we get the area {in terms 's'}= $$\frac{s^2}{\sqrt{3}}$$