Sign in
Please select an account to continue using cracku.in
↓ →
Three circles of equal radii touch (but not cross) each other externally. Two other circles, X and Y, are drawn such that both touch (but not cross) each of the three previous circles. If the radius of X is more than that of Y, the ratio of the radii of X and Y is
Let's take the radius of the original circles to be R and that of the circle in between the three circles to be r.

Joining the centres of the three circles, we will get an equilateral triangle or length 2R.
The distance between the circle's centre and the original circle's centre would be R+r.
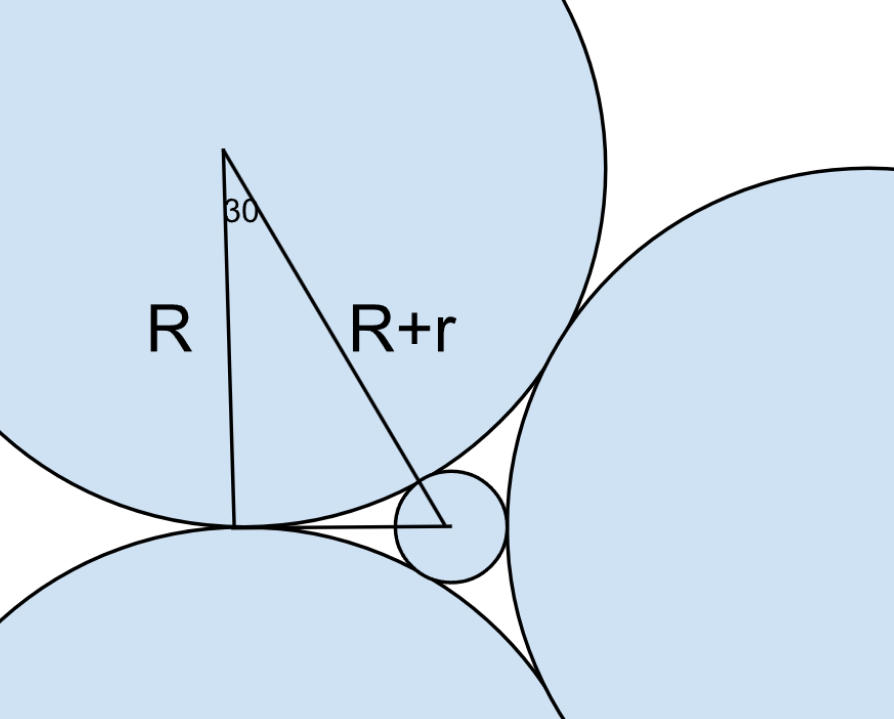
Using this right angle triangle, we can get the relation: $$\frac{R}{R+r}=\frac{\sqrt{\ 3}}{2}$$
We can take $$R=\sqrt{\ 3}a$$ and R+r as 2a, this would give us r as $$R=\left(2-\sqrt{\ 3}\right)a$$
The outer circle will have a radius of 2R+r
We need to find the ratio of $$\frac{2R+r}{r}$$
This will be equal to $$\frac{\left(2\sqrt{\ 3}+2-\sqrt{\ 3}\right)a}{\left(2-\sqrt{\ 3}\right)a}=\frac{2+\sqrt{\ 3}}{2-\sqrt{\ 3}}=4+3+4\sqrt{\ 3}=7+4\sqrt{\ 3}:1$$
Therefore, Option A is the correct answer.
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation