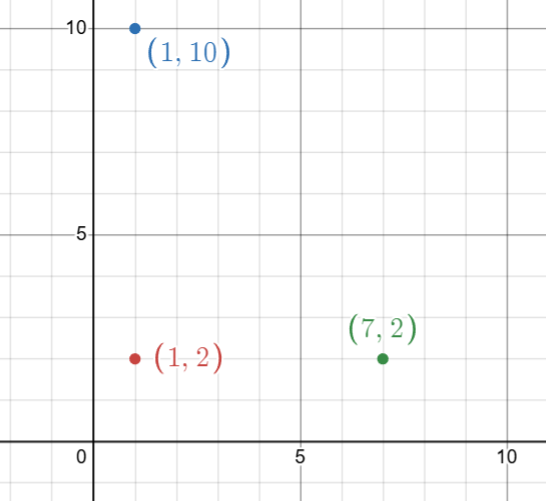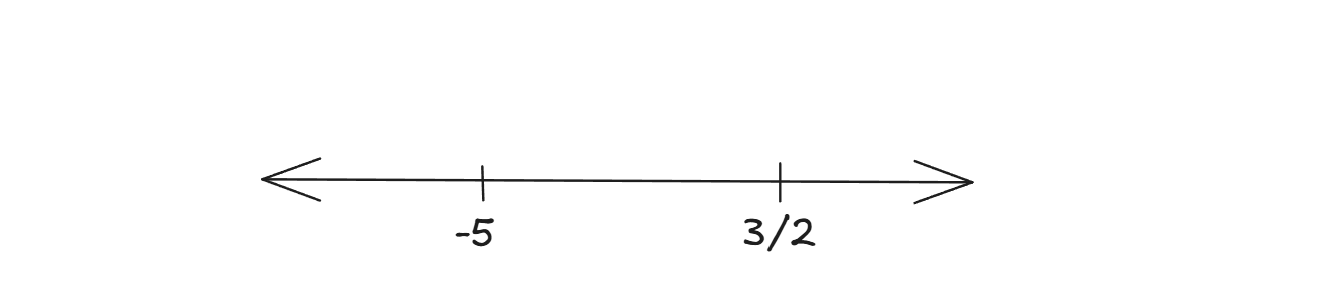CAT 2024 Slot 2 Quant Question Paper
For the following questions answer them individually
CAT 2024 Slot 2 Quant - Question 47
Bina incurs 19% loss when she sells a product at Rs. 4860 to Shyam, who in turn sells this product to Hari. If Bina would have sold this product to Shyam at the purchase price of Hari, she would have obtained 17% profit. Then, the profit, in rupees, made by Shyam is
789
456
123
0.-
Clear All
CAT 2024 Slot 2 Quant - Question 48
The coordinates of the three vertices of a triangle are: (1, 2), (7, 2), and (1, 10). Then the radius of the incircle of the triangle is
789
456
123
0.-
Clear All
CAT 2024 Slot 2 Quant - Question 49
A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes make up 40% of his stock. That day, he sells half of the mangoes, 96 bananas and 40% of the apples. At the end of the day, he ends up selling 50% of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is
789
456
123
0.-
Clear All
CAT 2024 Slot 2 Quant - Question 50
If a, b and c are positive real numbers such that $$a > 10 \geq b \geq c$$ and $$\cfrac{\log_8 (a + b)}{\log_2c} + \cfrac{\log_{27} (a - b)}{\log_3c} = \cfrac{2}{3}$$, then the greatest possible integer value of a is
789
456
123
0.-
Clear All
CAT 2024 Slot 2 Quant - Question 51
A function f maps the set of natural numbers to whole numbers, such that f(xy) = f(x)f(y) + f(x) + f(y) for all x, y and f(p) = 1 for every prime number p. Then, the value of f(160000) is
CAT 2024 Slot 2 Quant - Question 52
The roots $$\alpha, \beta$$ of the equation $$3x^2 + \lambda x - 1 = 0$$, satisfy $$\cfrac{1}{\alpha^2} + \cfrac{1}{\beta^2} = 15$$.
The value of $$(\alpha^3 + \beta^3)^2$$, is
CAT 2024 Slot 2 Quant - Question 53
When Rajesh's age was same as the present age of Garima, the ratio of their ages was 3 : 2. When Garima's age becomes the same as the present age of Rajesh, the ratio of the ages of Rajesh and Garima will become
CAT 2024 Slot 2 Quant - Question 54
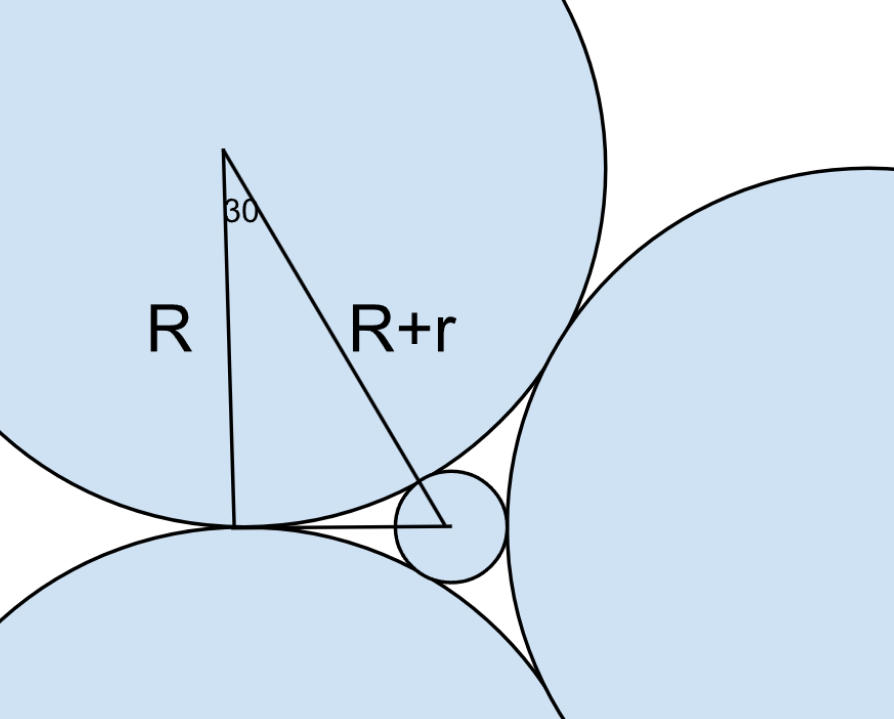
Three circles of equal radii touch (but not cross) each other externally. Two other circles, X and Y, are drawn such that both touch (but not cross) each of the three previous circles. If the radius of X is more than that of Y, the ratio of the radii of X and Y is
CAT 2024 Slot 2 Quant - Question 55
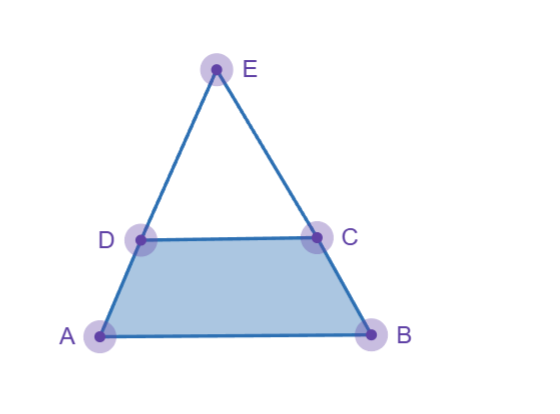
ABCD is a trapezium in which AB is parallel to CD. The sides AD and BC when extended, intersect at point E. If AB = 2 cm, CD = 1 cm, and perimeter of ABCD is 6 cm, then the perimeter, in cm, of $$\triangle AEB$$ is
CAT 2024 Slot 2 Quant - Question 56
A company has 40 employees whose names are listed in a certain order. In the year 2022, the average bonus of the first 30 employees was Rs. 40000, of the last 30 employees was Rs. 60000, and of the first 10 and last 10 employees together was Rs. 50000. Next year, the average bonus of the first 10 employees increased by 100%, of the last 10 employees increased by 200% and of the remaining employees was unchanged. Then, the average bonus, in rupees, of all the 40 employees together in the year 2023 was
CAT 2024 Slot 2 Quant - Question 57
Amal and Vimal together can complete a task in 150 days, while Vimal and Sunil together can complete the same task in 100 days. Amal starts working on the task and works for 75 days, then Vimal takes over and works for 135 days. Finally, Sunil takes over and completes the remaining task in 45 days. If Amal had started the task alone and worked on all days, Vimal had worked on every second day, and Sunil had worked on every third day, then the number of days required to complete the task would have been
789
456
123
0.-
Clear All
CAT 2024 Slot 2 Quant - Question 58
All the values of x satisfying the inequality $$\cfrac{1}{x + 5} \leq \cfrac{1}{2x - 3}$$ are
CAT 2024 Slot 2 Quant - Question 59
Anil invests Rs 22000 for 6 years in a scheme with 4% interest per annum, compounded half-yearly. Separately, Sunil invests a certain amount in the same scheme for 5 years, and then reinvests the entire amount he receives at the end of 5 years, for one year at 10% simple interest. If the amounts received by both at the end of 6 years are equal, then the initial investment, in rupees, made by Sunil is
CAT 2024 Slot 2 Quant - Question 60
A bus starts at 9 am and follows a fixed route every day. One day, it traveled at a constant speed of 60 km per hour and reached its destination 3.5 hours later than its scheduled arrival time. Next day, it traveled two-thirds of its route in one-third of its total scheduled travel time, and the remaining part of the route at 40 km per hour to reach just on time. The scheduled arrival time of the bus is
CAT 2024 Slot 2 Quant - Question 61
If $$m$$ and $$n$$ are natural numbers such that $$n > 1$$, and $$m^n = 2^{25} \times 3^{40}$$, then $$m - n$$ equals
CAT 2024 Slot 2 Quant - Question 62
When $$3^{333}$$ is divided by 11, the remainder is
CAT 2024 Slot 2 Quant - Question 63
If x and y are real numbers such that $$4x^2 + 4y^2 - 4xy - 6y + 3 = 0$$, then the value of $$(4x + 5y)$$ is
789
456
123
0.-
Clear All
CAT 2024 Slot 2 Quant - Question 64
If $$(x + 6\sqrt{2})^{\cfrac{1}{2}} - (x - 6\sqrt{2})^{\cfrac{1}{2}} = 2\sqrt{2}$$, then x equals
789
456
123
0.-
Clear All
CAT 2024 Slot 2 Quant - Question 65
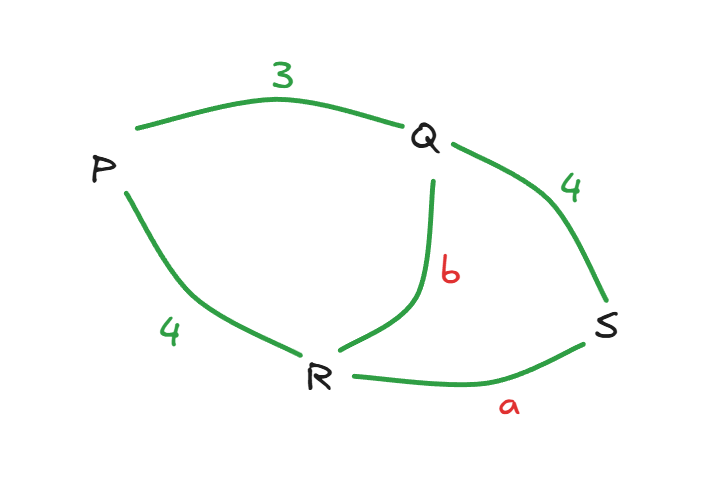
P, Q, R and S are four towns. One can travel between P and Q along 3 direct paths, between Q and S along 4 direct paths, and between P and R along 4 direct paths. There is no direct path between P and S, while there are few direct paths between Q and R, and between R and S. One can travel from P to S either via Q, or via R, or via Q followed by R, respectively, in exactly 62 possible ways. One can also travel from Q to R either directly, or via P, or via S, in exactly 27 possible ways. Then, the number of direct paths between Q and R is
789
456
123
0.-
Clear All
CAT 2024 Slot 2 Quant - Question 66
If x and y satisfy the equations $$\mid x \mid + x + y = 15$$ and $$x + \mid y \mid - y = 20$$, then $$(x - y)$$ equals
CAT 2024 Slot 2 Quant - Question 67
A vessel contained a certain amount of a solution of acid and water. When 2 litres of water was added to it, the new solution had 50% acid concentration. When 15 litres of acid was further added to this new solution, the final solution had 80% acid concentration. The ratio of water and acid in the original solution was
CAT 2024 Slot 2 Quant - Question 68
The sum of the infinite series $$\cfrac{1}{5}\left(\cfrac{1}{5} - \cfrac{1}{7}\right) + \left(\cfrac{1}{5}\right)^2 \left(\left(\cfrac{1}{5}\right)^2 - \left(\cfrac{1}{7}\right)^2\right) + \left(\cfrac{1}{5}\right)^3 \left(\left(\cfrac{1}{5}\right)^3 - \left(\cfrac{1}{7}\right)^3\right) + ......$$ is equal to
Two Factor Authentication
Incase of any issue contact support@cracku.in
CAT Quant Questions | CAT Quantitative Ability
CAT DILR Questions | LRDI Questions For CAT
CAT Verbal Ability Questions | VARC Questions For CAT
Also Read
Frequently Asked Questions
You can download the CAT 2024 Slot 2 Quant Question Paper PDF with detailed answers and solutions from Cracku.
Yes, video solutions are provided for every question in the CAT 2024 Slot 2 Quant paper to help you understand step by step.
Practicing the CAT 2024 Slot 2 Quant paper with solutions helps you learn the exam pattern, improve speed, and strengthen your Quant skills.
Yes, along with the CAT 2024 Slot 2 Quant paper, previous year CAT Quant papers are also available in PDF format for practice
Yes, the solutions explain simple methods and shortcuts to solve questions quickly and save time in the exam.