All the values of x satisfying the inequality $$\cfrac{1}{x + 5} \leq \cfrac{1}{2x - 3}$$ are

There are two critical points for the inequality to consider: x=-5 and x=3/2

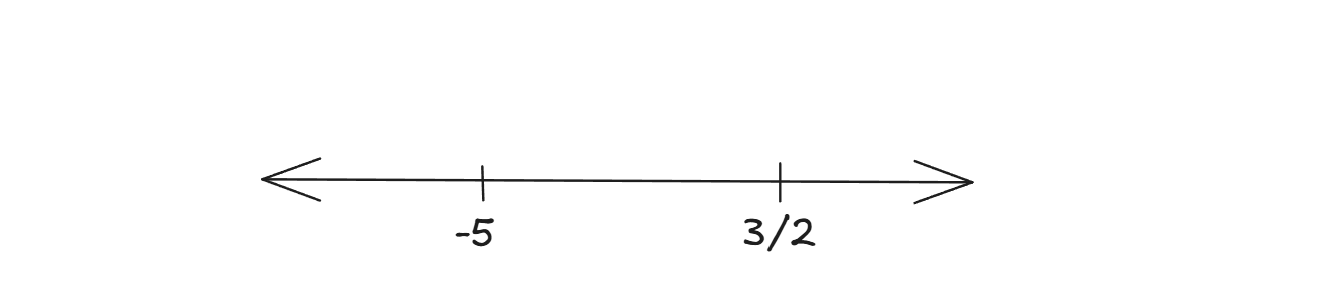
Region I: x is greater than 3/2
In this scenario, both the terms would be positive; cross-multiplying, we get the relation $$2x-3\le x+5$$
Giving the boundary $$x\le8$$, hence giving us the valid range as $$\frac{3}{2}<x\le8$$

Region II: $$-5<x<\frac{3}{2}$$
In this case, the right-hand side will be a negative value, and hence, the sign would change when multiplying, giving the inequality
$$2x-3\ge x+5$$
Which will give x>8, which is out of bounds for this region 

Another way is to put a value in the region to check for the validity of the inequality; by putting x=0, we could see that the inequality does not hold in this region 

Region III: x less than -5
In this scenario, both the terms are negative, essentially giving us the same boundary as region 1; we take the lower bounds, giving us that x has to be less than 5

Therefore, for the given inequality to hold true x<-5 or $$\frac{3}{2}<x\le8$$

Hence, Option A is the correct answer.