Sign in
Please select an account to continue using cracku.in
↓ →
Anil invests Rs 22000 for 6 years in a scheme with 4% interest per annum, compounded half-yearly. Separately, Sunil invests a certain amount in the same scheme for 5 years, and then reinvests the entire amount he receives at the end of 5 years, for one year at 10% simple interest. If the amounts received by both at the end of 6 years are equal, then the initial investment, in rupees, made by Sunil is
Let's take the amount invested by Sunil to be X.
The amount received by Anil at the end of 6 years would be $$22000\left(1+\frac{4}{2\times\ 100}\right)^{6\times\ 2}=22000\left(1.02\right)^{12}$$
The amount received by Sunil at the end of 5 years would be $$X\left(1.02\right)^{10}$$
In the 6th year, Sunil invests this at a simple interest of 10%, giving him an interest of $$X\left(1.02\right)^{10}\times\ 0.1$$
Giving the total amount with him at the end of 6 years to be $$X\left(1.02\right)^{10}\times\ \left(1+0.1\right)$$
Equating the final amount with Sunil and Anil, we get:
$$X\left(1.02\right)^{10}\times\ \left(1.1\right)=22000\left(1.02\right)^{12}$$
$$X=\frac{22000\left(1.02\right)^2}{1.1}=20808$$
Therefore, Option D is the correct answer.
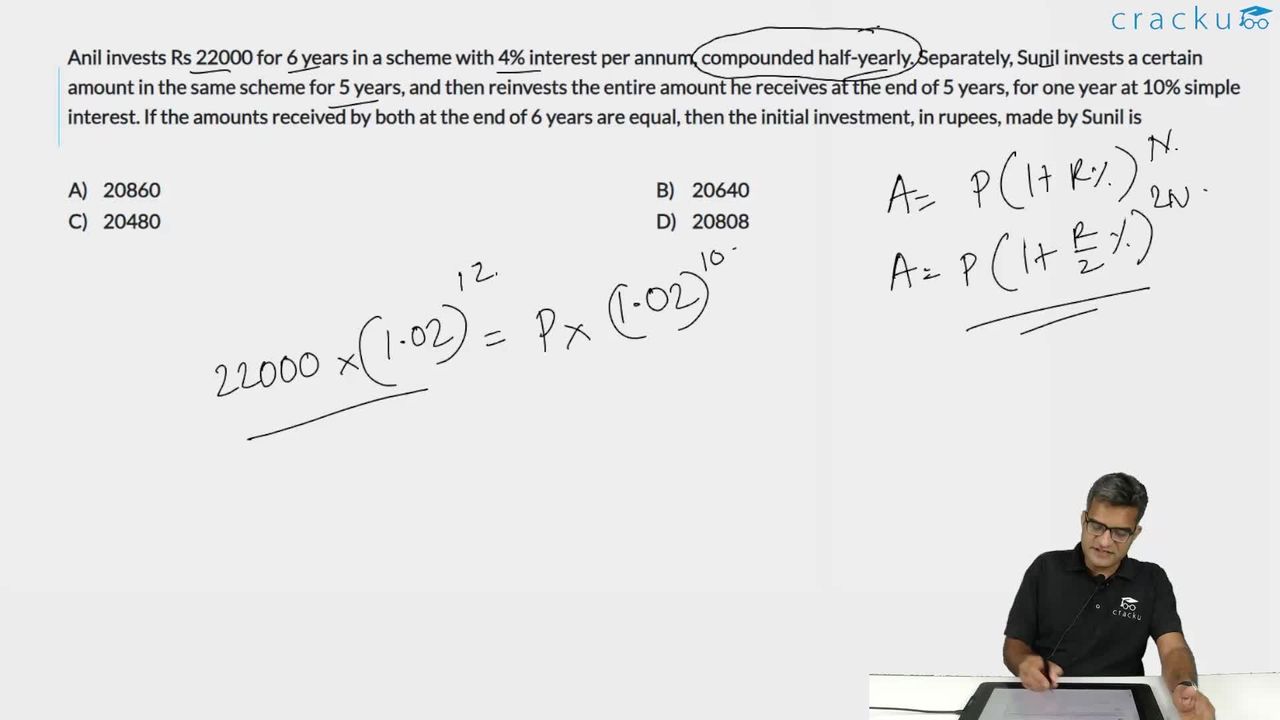
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation