Sign in
Please select an account to continue using cracku.in
↓ →
If $$(x + 6\sqrt{2})^{\cfrac{1}{2}} - (x - 6\sqrt{2})^{\cfrac{1}{2}} = 2\sqrt{2}$$, then x equals
Correct Answer: 11
Squaring on both sides, we get:
$$x+6\sqrt{\ 2}+x-6\sqrt{\ 2}-2\left(x^2-72\right)^{\frac{1}{2}}=8$$
$$x-\left(x^2-72\right)^{\frac{1}{2}}=4$$
Bringing x to the other side, we get:
$$-\left(x^2-72\right)^{\frac{1}{2}}=4-x$$
Squaring on both sides again, we get:
$$x^2-72=16+x^2-8x$$
$$8x=88$$
$$x=11$$
Therefore, 11 is the correct answer.
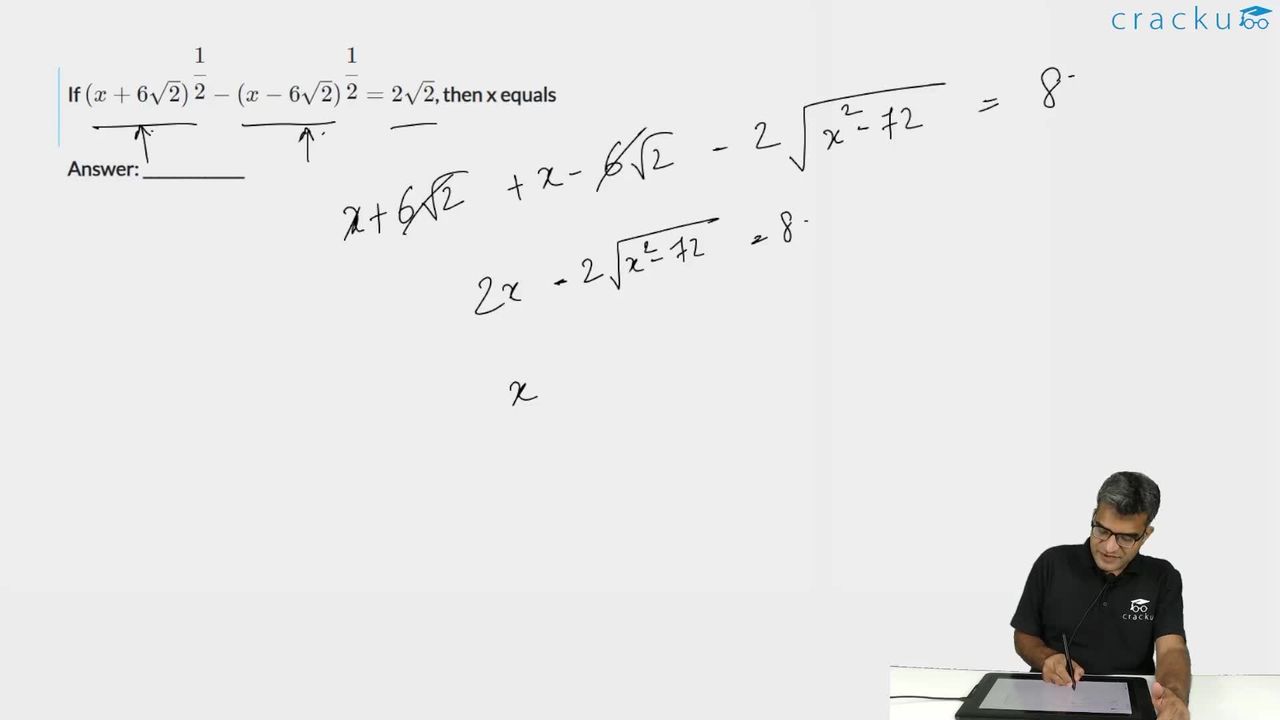
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation