Sign in
Please select an account to continue using cracku.in
↓ →
P, Q, R and S are four towns. One can travel between P and Q along 3 direct paths, between Q and S along 4 direct paths, and between P and R along 4 direct paths. There is no direct path between P and S, while there are few direct paths between Q and R, and between R and S. One can travel from P to S either via Q, or via R, or via Q followed by R, respectively, in exactly 62 possible ways. One can also travel from Q to R either directly, or via P, or via S, in exactly 27 possible ways. Then, the number of direct paths between Q and R is
Correct Answer: 7
Let's take the number of paths between Q and R to be b and the number of paths between R and S to be a
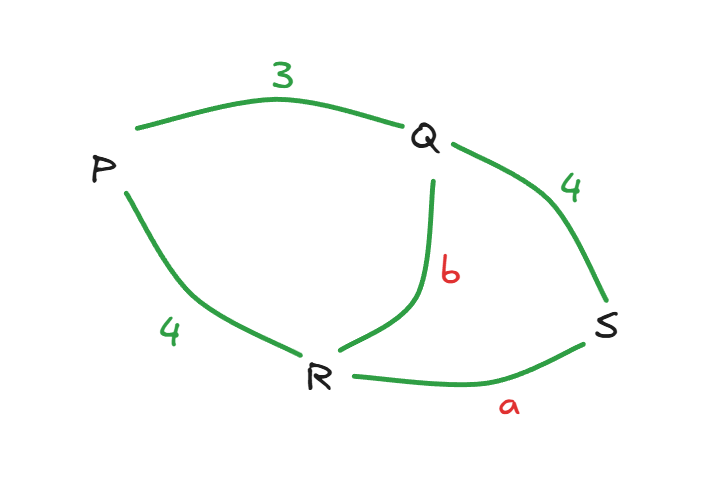
We are given the paths from P to S through R (which would be 4a), the paths from P to S through Q (which would be 12) and the paths from P to Q to R to S, which would be 3ab) is equal to 62
Giving the relation 4a+12+3ab = 62
Or 4a+3ab = 50
The paths from Q to R directly (which would be b), through P( which would be 12) and through S (which would be 4a) are 27
Giving the relation b+12+4a = 27
Or 4a+b = 15
Subtracting this equation from the first one we got, we get 3ab-b=35, or b(3a-1)=35
b can be 1, 3, 5 or 7
Substituting these values in the second equation, we see that it can not be 1 or 5, leaving only 3 or 7 as the possible values.
Substituting b as 3 in the first equation would give 13a=50, which is not true.
Substituting bas 7 in the first equation would give 25a= 50, which would give a=2
We are asked the number of paths from Q to R, which is b=7
Therefore, 7 is the correct answer.
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation