Sign in
Please select an account to continue using cracku.in
↓ →
A function f maps the set of natural numbers to whole numbers, such that f(xy) = f(x)f(y) + f(x) + f(y) for all x, y and f(p) = 1 for every prime number p. Then, the value of f(160000) is
Looking at the additional information about the prime numbers should make one realise that they are the key to solving the question.
f(16000) can be written as $$f\left(2^8\times\ 5^4\right)$$
Now, we can try to find these individual values:
For any prime p: f(p)=1
$$f\left(p^2\right)=f\left(p\right)f\left(p\right)+f\left(p\right)+f\left(p\right)=1+1+1=3$$
$$f\left(p^3\right)=f\left(p^2\right)f\left(p\right)+f\left(p^2\right)+f\left(p\right)=3+3+1=7$$
This way, we can find the function output for any prime number raised to a power.
We can see that each new exponent is twice the previous output +1, solving this way till prime raised to power 8
$$f\left(p^4\right)=7+7+1=15$$
$$f\left(p^5\right)=15+15+1=31$$
$$f\left(p^6\right)=31+31+1=63$$
$$f\left(p^7\right)=63+63+1=127$$
$$f\left(p^8\right)=127+127+1=255$$
Using these values in the original expression of $$f\left(2^8\times\ 5^4\right)=f\left(2^8\right)f\left(5^4\right)+f\left(2^8\right)+f\left(5^4\right)$$ we get
$$f\left(2^8\times\ 5^4\right)=\left(255\times\ 15\right)+255+15=4095$$
Therefore, Option A is the correct answer.
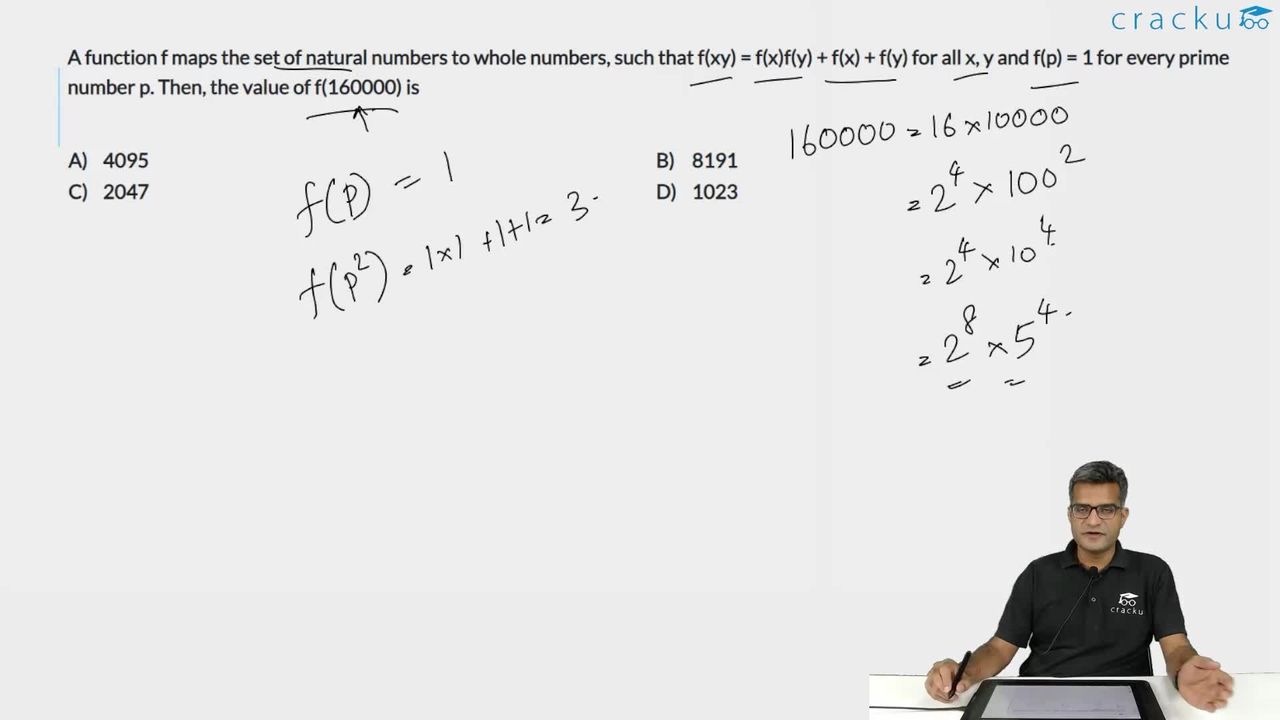
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation