Please enter the following details
On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
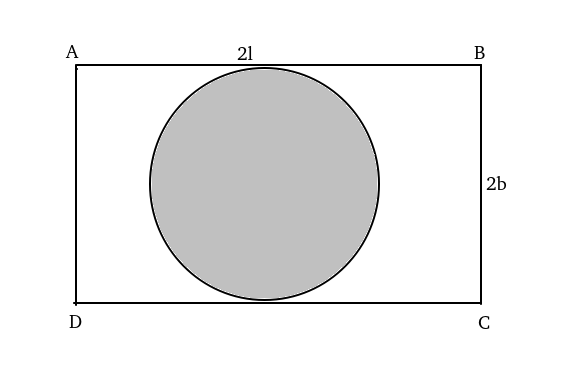
Let ABCD be the rectangle with length 2l and breadth 2b respectively.
Area of the circle i.e. area of painted region = $$\pi\ b^2$$.
Given, 4lb-$$\pi\ b^2$$=(2/3)$$\pi\ b^2$$.
=> 4lb=(5/3)$$\pi\ b^2$$.
=>l=$$\frac{5\pi}{12}b$$.
Given, 4lb=135 => 4*$$\frac{5\pi}{12}b^2$$=135 => b= $$\frac{9}{\sqrt{\ \pi\ }}$$
=> l=$$\frac{15}{4}\sqrt{\ \pi\ }$$
Perimeter of rectangle =4(l+b)=4($$\frac{15}{4}\sqrt{\ \pi\ }$$+$$\frac{9}{\sqrt{\ \pi\ }}$$ )=$$3\sqrt{\pi}(5+\frac{12}{\pi})$$.
Hence option A is correct.
Video Solution
Your Doubts
Drop Your File Here!
Ask Your Doubt
Drop Your File Here!
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
