CAT 2020 Slot 1 Quant Question Paper
For the following questions answer them individually
CAT 2020 Slot 1 Quant - Question 51
If Y is a negative number such that $$2^{Y^2({\log_{3}{5})}}=5^{\log_{2}{3}}$$, then Y equals to:
CAT 2020 Slot 1 Quant - Question 52
A gentleman decided to treat a few children in the following manner. He gives half of his total stock of toffees and one extra to the first child, and then the half of the remaining stock along with one extra to the second and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were there in his stock initially?
789
456
123
0.-
Clear All
CAT 2020 Slot 1 Quant - Question 53
How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7?
789
456
123
0.-
Clear All
CAT 2020 Slot 1 Quant - Question 54
The number of real-valued solutions of the equation $$2^{x}+2^{-x}=2-(x-2)^{2}$$ is:
CAT 2020 Slot 1 Quant - Question 55
How many disticnt positive integer-valued solutions exist to the equation $$(x^{2}-7x+11)^{(x^{2}-13x+42)}=1$$ ?
CAT 2020 Slot 1 Quant - Question 56
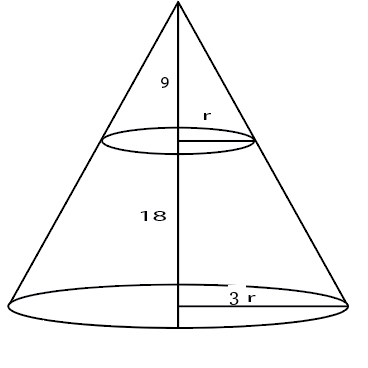
A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
CAT 2020 Slot 1 Quant - Question 57
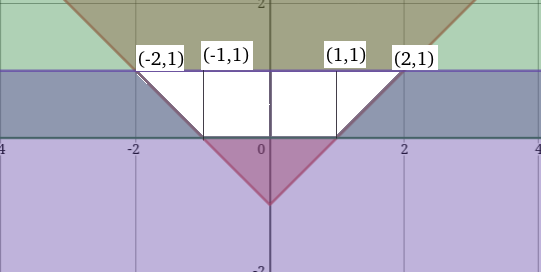
The area of the region satisfying the inequalities $$\mid x\mid-y\leq1,y\geq0$$ and $$y\leq1$$ is
789
456
123
0.-
Clear All
CAT 2020 Slot 1 Quant - Question 58
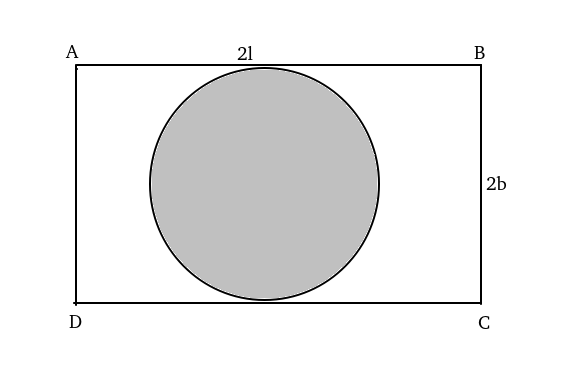
On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
CAT 2020 Slot 1 Quant - Question 59
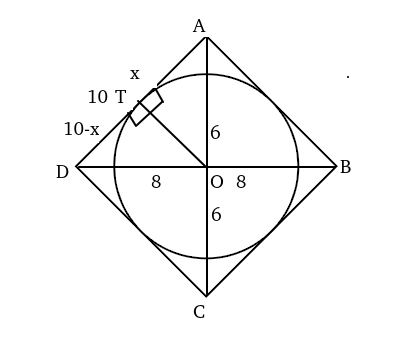
A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
CAT 2020 Slot 1 Quant - Question 60
Among 100 students, $$x_1$$ have birthdays in January, $$X_2$$ have birthdays in February, and so on. If $$x_0=max(x_1,x_2,....,x_{12})$$, then the smallest possible value of $$x_0$$ is
CAT 2020 Slot 1 Quant - Question 61
A straight road connects points A and B. Car 1 travels from A to B and Car 2 travels from B to A, both leaving at the same time. After meeting each other, they take 45 minutes and 20 minutes, respectively, to complete their journeys. If Car 1 travels at the speed of 60 km/hr, then the speed of Car 2, in km/hr, is
CAT 2020 Slot 1 Quant - Question 62
A person spent Rs 50000 to purchase a desktop computer and a laptop computer. He sold the desktop at 20% profit and the laptop at 10% loss. If overall he made a 2% profit then the purchase price, in rupees, of the desktop is
789
456
123
0.-
Clear All
CAT 2020 Slot 1 Quant - Question 63
A solution, of volume 40 litres, has dye and water in the proportion 2 : 3. Water is added to the solution to change this proportion to 2 : 5. If one fourths of this diluted solution is taken out, how many litres of dye must be added to the remaining solution to bring the proportion back to 2 : 3?
789
456
123
0.-
Clear All
CAT 2020 Slot 1 Quant - Question 64
If $$x=(4096)^{7+4\sqrt{3}}$$, then which of the following equals to 64?
CAT 2020 Slot 1 Quant - Question 65
An alloy is prepared by mixing three metals A, B and C in the proportion 3 : 4 : 7 by volume. Weights of the same volume of the metals A. B and C are in the ratio 5 : 2 : 6. In 130 kg of the alloy, the weight, in kg. of the metal C is
CAT 2020 Slot 1 Quant - Question 66
The number of distinct real roots of the equation $$(x+\frac{1}{x})^{2}-3(x+\frac{1}{x})+2=0$$ equals
789
456
123
0.-
Clear All
CAT 2020 Slot 1 Quant - Question 67
If $$\log_{4}{5}=(\log_{4}{y})(\log_{6}{\sqrt{5}})$$, then y equals
789
456
123
0.-
Clear All
CAT 2020 Slot 1 Quant - Question 68
Leaving home at the same time, Amal reaches the office at 10:15 am if he travels at 8 km/hr, and at 9:40 am if he travels at 15 km/hr. Leaving home at 9.10 am, at what speed, in km/hr, must he travel so as to reach office exactly at 10 am?
CAT 2020 Slot 1 Quant - Question 69
A train travelled at one-thirds of its usual speed, and hence reached the destination 30 minutes after the scheduled time. On its return journey, the train initially travelled at its usual speed for 5 minutes but then stopped for 4 minutes for an emergency. The percentage by which the train must now increase its usual speed so as to reach the destination at the scheduled time, is nearest to
CAT 2020 Slot 1 Quant - Question 70
The mean of all 4-digit even natural numbers of the form 'aabb',where $$a>0$$, is
CAT 2020 Slot 1 Quant - Question 71
Two persons are walking beside a railway track at respective speeds of 2 and 4 km per hour in the same direction. A train came from behind them and crossed them in 90 and 100 seconds, respectively. The time, in seconds, taken by the train to cross an electric post is nearest to
CAT 2020 Slot 1 Quant - Question 72
If a, b and c are positive integers such that ab = 432, bc = 96 and c < 9, then the smallest possible value of a + b + c is
CAT 2020 Slot 1 Quant - Question 73
In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to
CAT 2020 Slot 1 Quant - Question 74
Veeru invested Rs 10000 at 5% simple annual interest, and exactly after two years, Joy invested Rs 8000 at 10% simple annual interest. How many years after Veeru’s investment, will their balances, i.e., principal plus accumulated interest, be equal?
789
456
123
0.-
Clear All
CAT 2020 Slot 1 Quant - Question 75
If $$f(5+x)=f(5-x)$$ for every real x, and $$f(x)=0$$ has four distinct real roots, then the sum of these roots is
CAT 2020 Slot 1 Quant - Question 76
Let A, B and C be three positive integers such that the sum of A and the mean of B and C is 5. In addition, the sum of B and the mean of A and C is 7. Then the sum of A and B is
Two Factor Authentication
Incase of any issue contact support@cracku.in