Sign in
Please select an account to continue using cracku.in
↓ →
On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
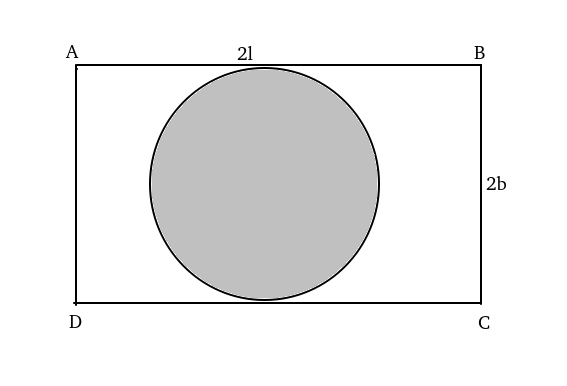
Let ABCD be the rectangle with length 2l and breadth 2b respectively.
Area of the circle i.e. area of painted region = $$\pi\ b^2$$.
Given, 4lb-$$\pi\ b^2$$=(2/3)$$\pi\ b^2$$.
=> 4lb=(5/3)$$\pi\ b^2$$.
=>l=$$\frac{5\pi}{12}b$$.
Given, 4lb=135 => 4*$$\frac{5\pi}{12}b^2$$=135 => b= $$\frac{9}{\sqrt{\ \pi\ }}$$
=> l=$$\frac{15}{4}\sqrt{\ \pi\ }$$
Perimeter of rectangle =4(l+b)=4($$\frac{15}{4}\sqrt{\ \pi\ }$$+$$\frac{9}{\sqrt{\ \pi\ }}$$ )=$$3\sqrt{\pi}(5+\frac{12}{\pi})$$.
Hence option A is correct.

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation