Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 56
A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
Solution
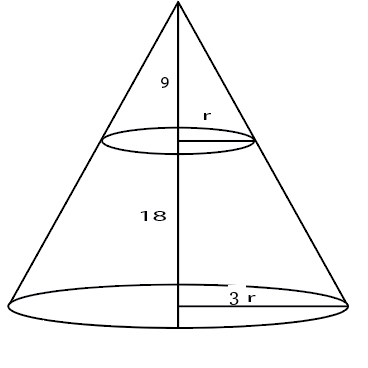
Let the base radius be 3r.
Height of upper cone is 9 so, by symmetry radius of upper cone will be r.
Volume of frustum=$$\frac{\pi}{3}\left(9r^2\cdot27-r^2.9\right)$$
Volume of upper cone = $$\frac{\pi}{3}.r^2.9$$
Difference= $$\frac{\pi}{3}\cdot9\cdot r^2\cdot25=225$$ => $$\frac{\pi}{3}\cdot r^2=1$$
Volume of larger cone = $$\frac{\pi}{3}\cdot9r^2\cdot27=243$$
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
CAT Quant Questions | CAT Quantitative Ability
CAT Linear Equations QuestionsCAT Mensuration QuestionsCAT Time And Work QuestionsCAT Logarithms QuestionsCAT Percentages Questions
CAT DILR Questions | LRDI Questions For CAT
CAT Venn Diagrams QuestionsCAT Puzzles QuestionsCAT Games and Tournamnents QuestionsCAT Data Interpretation QuestionsCAT Truth Lie Concept Questions
