CAT WhatsApp Group
Sign in
Please select an account to continue using cracku.in
↓ →
CAT WhatsApp Group
A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
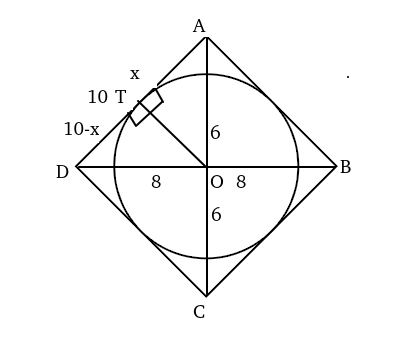
Let the length of radius be 'r'.
From the above diagram,
$$x^2+r^2=6^2\ $$....(i)
$$\left(10-x\right)^2+r^2=8^2\ $$----(ii)
Subtracting (i) from (ii), we get:
x=3.6 => $$r^2=36-\left(3.6\right)^2$$ ==> $$r^2=36-\left(3.6\right)^2\ =23.04$$.
Area of circle = $$\pi\ r^2=23.04\pi\ $$
Area of rhombus= 1/2*d1*d2=1/2*12*16=96.
.'. Ratio of areas = 23.04$$\pi\ $$/96=$$\frac{6\pi}{25}$$
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation
Ask our AI anything
AI can make mistakes. Please verify important information.
AI can make mistakes. Please verify important information.
