On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is

Let us draw the diagram according to the available information.

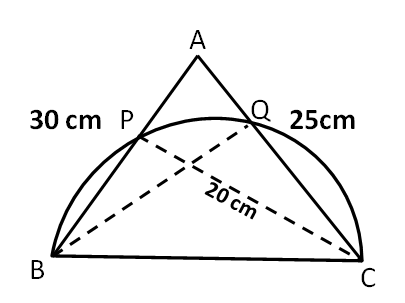
We can see that triangle BPC and BQC are inscribed inside a semicircle. Hence, we can say that

$$\angle$$ BPC = $$\angle$$ BQC = 90°

Therefore, we can say that BQ  $$\perp$$ AC and CP $$\perp$$ AB.

In triangle ABC,

Area of triangle = (1/2)*Base*Height = (1/2)*AB*CP = (1/2)*AC*BQ

$$\Rightarrow$$ BQ = $$\dfrac{AB*CP}{AC}$$ = $$\dfrac{30*20}{25}$$ = 24 cm.