Sign in
Please select an account to continue using cracku.in
↓ →
In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is
It is given that AD and BE are medians which are perpendicular to each other.
The lengths of AD and BE are 12cm and 9cm respectively.
It is known that the centroid G divides the median in the ratio of 2:1
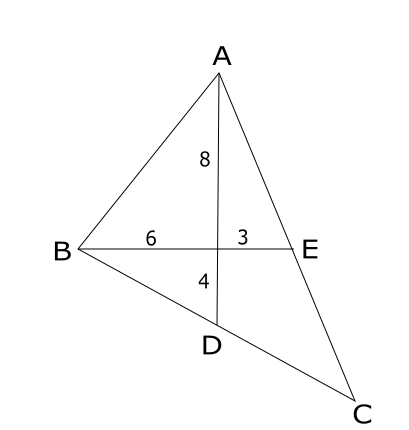
Area of $$\triangle$$ ABC = 2* Area of the triangle ABD
Area of $$\triangle\ $$ABD = Area of $$\triangle\ $$ AGB + Area of $$\triangle\ $$ BGD
Since $$\angle\ AGB\ =\ \angle\ BGD\ =\ 90$$ (Given)
Area of $$\triangle\ $$ AGB = $$\ \frac{\ 1}{2}\times\ 8\times\ 6$$ = 24
Area of $$\triangle\ $$ BGD = $$\ \frac{\ 1}{2}\times\ 6\times\ 4$$ = 12
Area of $$\triangle\ $$ABD = 24+12=36
Area of $$\triangle\ ABC\ =\ 2\times\ 36=72$$

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation