CAT 2019 Slot 2 Quant Question Paper
For the following questions answer them individually
CAT 2019 Slot 2 Quant - Question 67
The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers?
CAT 2019 Slot 2 Quant - Question 68
Amal invests Rs 12000 at 8% interest, compounded annually, and Rs 10000 at 6% interest, compounded semi-annually, both investments being for one year. Bimal invests his money at 7.5% simple interest for one year. If Amal and Bimal get the same amount of interest, then the amount, in Rupees, invested by Bimal is
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 69
What is the largest positive integer n such that $$\frac{n^2 + 7n + 12}{n^2 - n - 12}$$ is also a positive integer?
CAT 2019 Slot 2 Quant - Question 70
How many pairs (m, n) of positive integers satisfy the equation $$m^2 + 105 = n^2$$?
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 71
Two ants A and B start from a point P on a circle at the same time, with A moving clock-wise and B moving anti-clockwise. They meet for the first time at 10:00 am when A has covered 60% of the track. If A returns to P at 10:12 am, then B returns to P at
CAT 2019 Slot 2 Quant - Question 72
Let $$a_1, a_2, ...$$ be integers such that
$$a_1 - a_2 + a_3 - a_4 + .... + (-1)^{n - 1} a_n = n,$$ for all $$n \geq 1.$$
Then $$a_{51} + a_{52} + .... + a_{1023}$$ equals
CAT 2019 Slot 2 Quant - Question 73
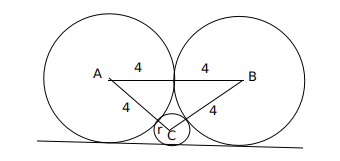
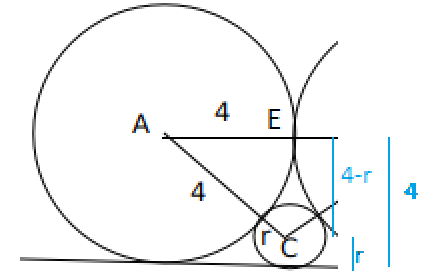
Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
CAT 2019 Slot 2 Quant - Question 74
Let A be a real number. Then the roots of the equation $$x^2 - 4x - log_{2}{A} = 0$$ are real and distinct if and only if
CAT 2019 Slot 2 Quant - Question 75
The quadratic equation $$x^2 + bx + c = 0$$ has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of $$b^2 + c$$?
CAT 2019 Slot 2 Quant - Question 76
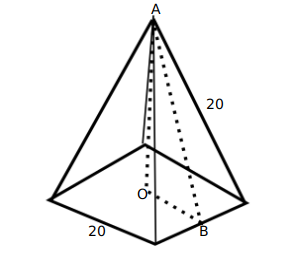
The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is
CAT 2019 Slot 2 Quant - Question 77
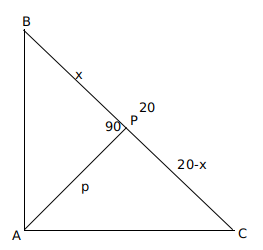
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
CAT 2019 Slot 2 Quant - Question 78
If x is a real number, then $$\sqrt{\log_{e}{\frac{4x - x^2}{3}}}$$ is a real number if and only if
CAT 2019 Slot 2 Quant - Question 79
If $$5^x - 3^y = 13438$$ and $$5^{x - 1} + 3^{y + 1} = 9686$$, then x + y equals
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 80
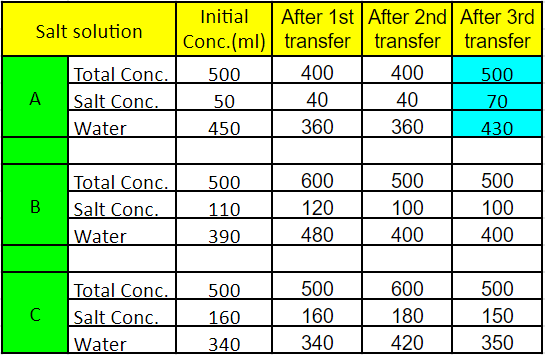
The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is
CAT 2019 Slot 2 Quant - Question 81
A cyclist leaves A at 10 am and reaches B at 11 am. Starting from 10:01 am, every minute a motorcycle leaves A and moves towards B. Forty-five such motorcycles reach B by 11 am. All motorcycles have the same speed. If the cyclist had doubled his speed, how many motorcycles would have reached B by the time the cyclist reached B?
CAT 2019 Slot 2 Quant - Question 82
A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is
CAT 2019 Slot 2 Quant - Question 83
The real root of the equation $$2^{6x} + 2^{3x + 2} - 21 = 0$$ is
CAT 2019 Slot 2 Quant - Question 84
How many factors of $$2^4 \times 3^5 \times 10^4$$ are perfect squares which are greater than 1?
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 85
In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits. Then, the largest possible value of the fourth digit is
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 86
John jogs on track A at 6 kmph and Mary jogs on track B at 7.5 kmph. The total length of tracks A and B is 325 metres. While John makes 9 rounds of track A, Mary makes 5 rounds of track B. In how many seconds will Mary make one round of track A?
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 87
In 2010, a library contained a total of 11500 books in two categories - fiction and nonfiction. In 2015, the library contained a total of 12760 books in these two categories. During this period, there was 10% increase in the fiction category while there was 12% increase in the non-fiction category. How many fiction books were in the library in 2015?
CAT 2019 Slot 2 Quant - Question 88
John gets Rs 57 per hour of regular work and Rs 114 per hour of overtime work. He works altogether 172 hours and his income from overtime hours is 15% of his income from regular hours. Then, for how many hours did he work overtime?
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 89
If $$(2n + 1) + (2n + 3) + (2n + 5) + ... + (2n + 47) = 5280$$, then whatis the value of $$1 + 2 + 3 + .. + n?$$
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 90
A shopkeeper sells two tables, each procured at cost price p, to Amal and Asim at a profit of 20% and at a loss of 20%, respectively. Amal sells his table to Bimal at a profit of 30%, while Asim sells his table to Barun at a loss of 30%. If the amounts paid by Bimal and Barun are x and y, respectively, then (x − y) / p equals
CAT 2019 Slot 2 Quant - Question 91
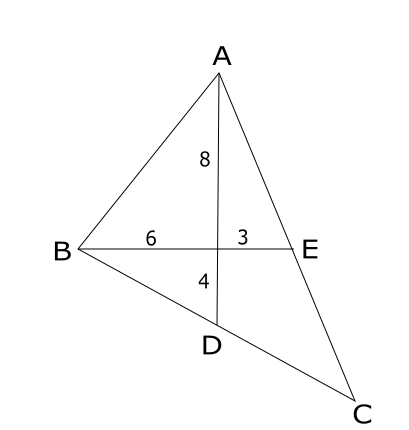
In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is
CAT 2019 Slot 2 Quant - Question 92
The number of common terms in the two sequences: 15, 19, 23, 27, . . . . , 415 and 14, 19, 24, 29, . . . , 464 is
CAT 2019 Slot 2 Quant - Question 93
Let a, b, x, y be real numbers such that $$a^2 + b^2 = 25, x^2 + y^2 = 169$$, and $$ax + by = 65$$. If $$k = ay - bx$$, then
CAT 2019 Slot 2 Quant - Question 94
Mukesh purchased 10 bicycles in 2017, all at the same price. He sold six of these at a profit of 25% and the remaining four at a loss of 25%. If he made a total profit of Rs. 2000, then his purchase price of a bicycle, in Rupees, was
CAT 2019 Slot 2 Quant - Question 95
In an examination, the score of A was 10% less than that of B, the score of B was 25% more than that of C, and the score of C was 20% less than that of D. If A scored 72, then the score of D was
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 96
The salaries of Ramesh, Ganesh and Rajesh were in the ratio 6:5:7 in 2010, and in the ratio 3:4:3 in 2015. If Ramesh’s salary increased by 25% during 2010-2015, then the percentage increase in Rajesh’s salary during this period is closest to
CAT 2019 Slot 2 Quant - Question 97
Let A and B be two regular polygons having a and b sides, respectively. If b = 2a and each interior angle of B is $$\frac{3}{2}$$ times each interior angle of A, then each interior angle, in degrees, of a regular polygon with a + b sides is
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 98
Let f be a function such that f (mn) = f (m) f (n) for every positive integers m and n. If f (1), f (2) and f (3) are positive integers, f (1) < f (2), and f (24) = 54, then f (18) equals
789
456
123
0.-
Clear All
CAT 2019 Slot 2 Quant - Question 99
Anil alone can do a job in 20 days while Sunil alone can do it in 40 days. Anil starts the job, and after 3 days, Sunil joins him. Again, after a few more days, Bimal joins them and they together finish the job. If Bimal has done 10% of the job, then in how many days was the job done?
CAT 2019 Slot 2 Quant - Question 100
In an examination, Rama's score was one-twelfth of the sum of the scores of Mohan and Anjali. After a review, the score of each of them increased by 6. The revised scores of Anjali, Mohan, and Rama were in the ratio 11:10:3. Then Anjali's score exceeded Rama's score by
Two Factor Authentication
Incase of any issue contact support@cracku.in