Sign in
Please select an account to continue using cracku.in
↓ →
Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
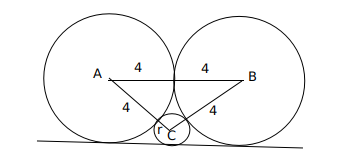
Let 'h' be the height of the triangle ABC, semiperimeter(S) $$= \frac{4+4+r+4+4+r}{2} = 8+r$$,
$$a=4+r, b=4+r, c=8$$
Area of triangle ABC $$=\ \ \sqrt{\ s\cdot\left(s-a\right)\left(s-b\right)\left(s-c\right)}=$$
$$= \sqrt{\left(\ 8+r\right)\times\ 4\times\ 4\times\ r}$$ = $$\ \frac{\ 1}{2}\times\ \left(4+4\right)\times\ height$$
Height (h) = $$\sqrt{\ \left(8+r\right)r}$$
Now, $$ h + r = 4 \longrightarrow \sqrt{\ \left(8+r\right)r} + r = 4$$ (Considering the height of the triangle)
$$\sqrt{\ \left(8+r\right)r}$$=4-r
16r=16
r=1
Alternatively,
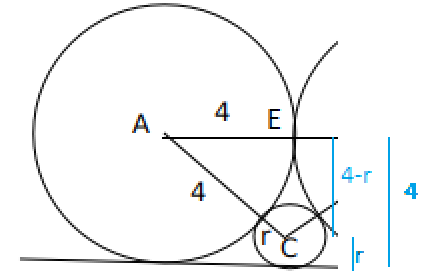
$$\text{AE}^@+\text{EC}^2=\text{AC}^2 \longrightarrow 4^2+\left(4-r\right)^2 = \left(4+r\right)^2 \longrightarrow\ \longrightarrow\ \longrightarrow\ r=1$$

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation