CAT WhatsApp Group
Sign in
Please select an account to continue using cracku.in
↓ →
CAT WhatsApp Group
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
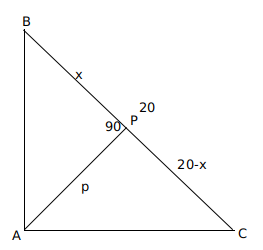
Let p be the length of AP.
It is given that $$\angle\ BAC\ =90\ $$ and $$\angle\ APC\ =90\ $$
Let $$\angle\ ABC\ =\theta\ $$, then $$\angle\ BAP\ =90-\theta\ $$ and $$\angle\ BCA\ =90-\theta\ $$
So $$\angle\ PAC\ =\theta\ $$
Triangles BPA and APC are similar
$$p^2=x\left(20-x\right)$$
We have to maximize the value of p, which will be maximum when x=20-x
x=10
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Book Free CAT Mentorship
Get personalized CAT strategy from a 99%iler
500+ students mentored
OTP Verification
Enter the 6-digit code sent to your phone
Booking Summary
Enter OTP
Didn't receive the OTP?
Educational materials for CAT preparation
Ask our AI anything
AI can make mistakes. Please verify important information.
AI can make mistakes. Please verify important information.
