The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is

It is given that the base of the pyramid is square and each of the four sides are equilateral triangles.

Length of each side of the equilateral triangle = 20cm

Since the side of the triangle will be common to the square as well, the side of the square = 20cm

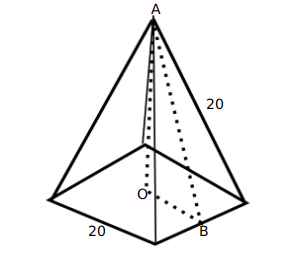
Let h be the vertical height of the pyramid ie OA

OB = 10 since it is half the side of the square 

AB is the height of the equilateral triangle i.e 10$$\sqrt{\ 3}$$

AOB is a right angle, so applying the Pythagorean formula, we get

$$OA^2+ OB^2= AB^2$$

$$h^2$$ + 100= 300

h=10$$\sqrt{\ 2}$$