CAT 2024 Slot 3 Quant Question Paper
For the following questions answer them individually
CAT 2024 Slot 3 Quant - Question 47
In a group of 250 students, the percentage of girls was at least 44% and at most 60%.The rest of the students were boys. Each student opted for either swimming or running or both. If 50% of the boys and 80% of the girls opted for swimming while 70%of the boys and 60% of the girls opted for running, then the minimum and maximum possible number of students who opted for both swimming and running, are
CAT 2024 Slot 3 Quant - Question 48
If $$(a + b\sqrt{3})^2 = 52 + 30\sqrt{3}$$, where a and b are natural numbers, then $$a + b$$ equals
CAT 2024 Slot 3 Quant - Question 49
The average of three distinct real numbers is 28. If the smallest number is increased by 7 and the largest number is reduced by 10, the order of the numbers remains unchanged, and the new arithmetic mean becomes 2 more than the middle number, while the difference between the largest and the smallest numbers becomes 64.Then, the largest number in the original set of three numbers is
789
456
123
0.-
Clear All
CAT 2024 Slot 3 Quant - Question 50
If $$10^{68}$$ is divided by 13, the remainder is
CAT 2024 Slot 3 Quant - Question 51
Sam can complete a job in 20 days when working alone. Mohit is twice as fast as Sam and thrice as fast as Ayna in the same job. They undertake a job with an arrangement where Sam and Mohit work together on the first day, Sam and Ayna on the second day, Mohit and Ayna on the third day, and this three-day pattern is repeated till the work gets completed. Then, the fraction of total work done by Sam is
CAT 2024 Slot 3 Quant - Question 52
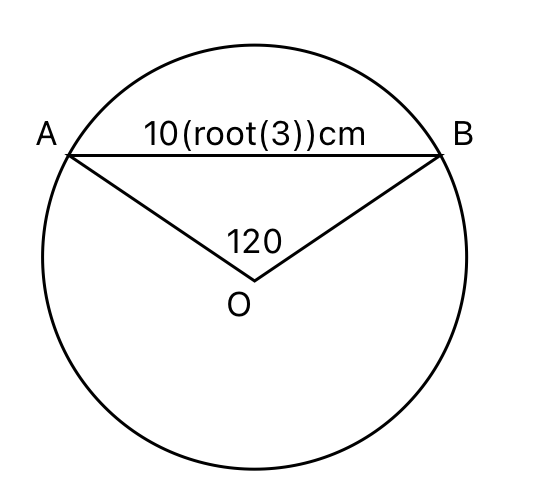
A circular plot of land is divided into two regions by a chord of length $$10\sqrt{3}$$ meters such that the chord subtends an angle of 120° at the center. Then, the area, in square meters, of the smaller region is
CAT 2024 Slot 3 Quant - Question 53
Consider the sequence $$t_1 = 1, t_2 = -1$$ and $$t_n = \left(\cfrac{n - 3}{n - 1}\right)t_{n - 2}$$ for $$n \geq 3$$. Then, the value of the sum $$\cfrac{1}{t_2} + \cfrac{1}{t_4} + \cfrac{1}{t_6} + ....... +\cfrac{1}{t_{2022}} + \cfrac{1}{t_{2024}}$$, is
CAT 2024 Slot 3 Quant - Question 54
The number of distinct real values of x, satisfying the equation $$max \left\{x, 2\right\} - min\left\{x, 2\right\} = \mid x + 2 \mid - \mid x - 2 \mid$$, is
789
456
123
0.-
Clear All
CAT 2024 Slot 3 Quant - Question 55
Aman invests Rs 4000 in a bank at a certain rate of interest, compounded annually. If the ratio of the value of the investment after 3 years to the value of the investment after 5 years is 25 : 36, then the minimum number of years required for the value of the investment to exceed Rs 20000 is
789
456
123
0.-
Clear All
CAT 2024 Slot 3 Quant - Question 56
The sum of all distinct real values of x that satisfy the equation $$10^x + \cfrac{4}{10^x} = \cfrac{81}{2}$$, is
CAT 2024 Slot 3 Quant - Question 57
A train travelled a certain distance at a uniform speed. Had the speed been 6 km per hour more, it would have needed 4 hours less. Had the speed been 6 km per hour less, it would have needed 6 hours more. The distance, in km, travelled by the train is
CAT 2024 Slot 3 Quant - Question 58
If $$3^a = 4, 4^b = 5, 5^c = 6, 6^d = 7, 7^e = 8$$ and $$8^f = 9$$, then the value of the product abcdef is
789
456
123
0.-
Clear All
CAT 2024 Slot 3 Quant - Question 59
Gopi marks a price on a product in order to make 20% profit. Ravi gets 10% discount on this marked price, and thus saves Rs 15. Then, the profit, in rupees, made by Gopi by selling the product to Ravi, is
CAT 2024 Slot 3 Quant - Question 60
A certain amount of water was poured into a 300 litre container and the remaining portion of the container was filled with milk. Then an amount of this solution was taken out from the container which was twice the volume of water that was earlier poured into it, and water was poured to refill the container again. If the resulting solution contains 72% milk, then the amount of water, in litres, that was initially poured into the container was
789
456
123
0.-
Clear All
CAT 2024 Slot 3 Quant - Question 61
A regular octagon ABCDEFGH has sides of length 6 cm each. Then the area, in sq. cm, of the square ACEG is
CAT 2024 Slot 3 Quant - Question 62
The number of distinct integer solutions (x, y) of the equation $$\mid x + y \mid + \mid x - y \mid = 2$$, is
789
456
123
0.-
Clear All
CAT 2024 Slot 3 Quant - Question 63
For any non-zero real number x, let $$f(x) + 2f \left(\cfrac{1}{x}\right) = 3x$$. Then, the sum of all possible values of x for which $$f(x) = 3$$, is
CAT 2024 Slot 3 Quant - Question 64
For some constant real numbers p, k and a, consider the following system of linear equations in x and y:
px - 4y = 2
3x + ky= a
A necessary condition for the system to have no solution for (x, y ), is
CAT 2024 Slot 3 Quant - Question 65
Rajesh and Vimal own 20 hectares and 30 hectares of agricultural land, respectively, which are entirely covered by wheat and mustard crops. The cultivation area of wheat and mustard in the land owned by Vimal are in the ratio of 5 : 3. If the total cultivation area of wheat and mustard are in the ratio 11 : 9, then the ratio of cultivation area of wheat and mustard in the land owned by Rajesh is
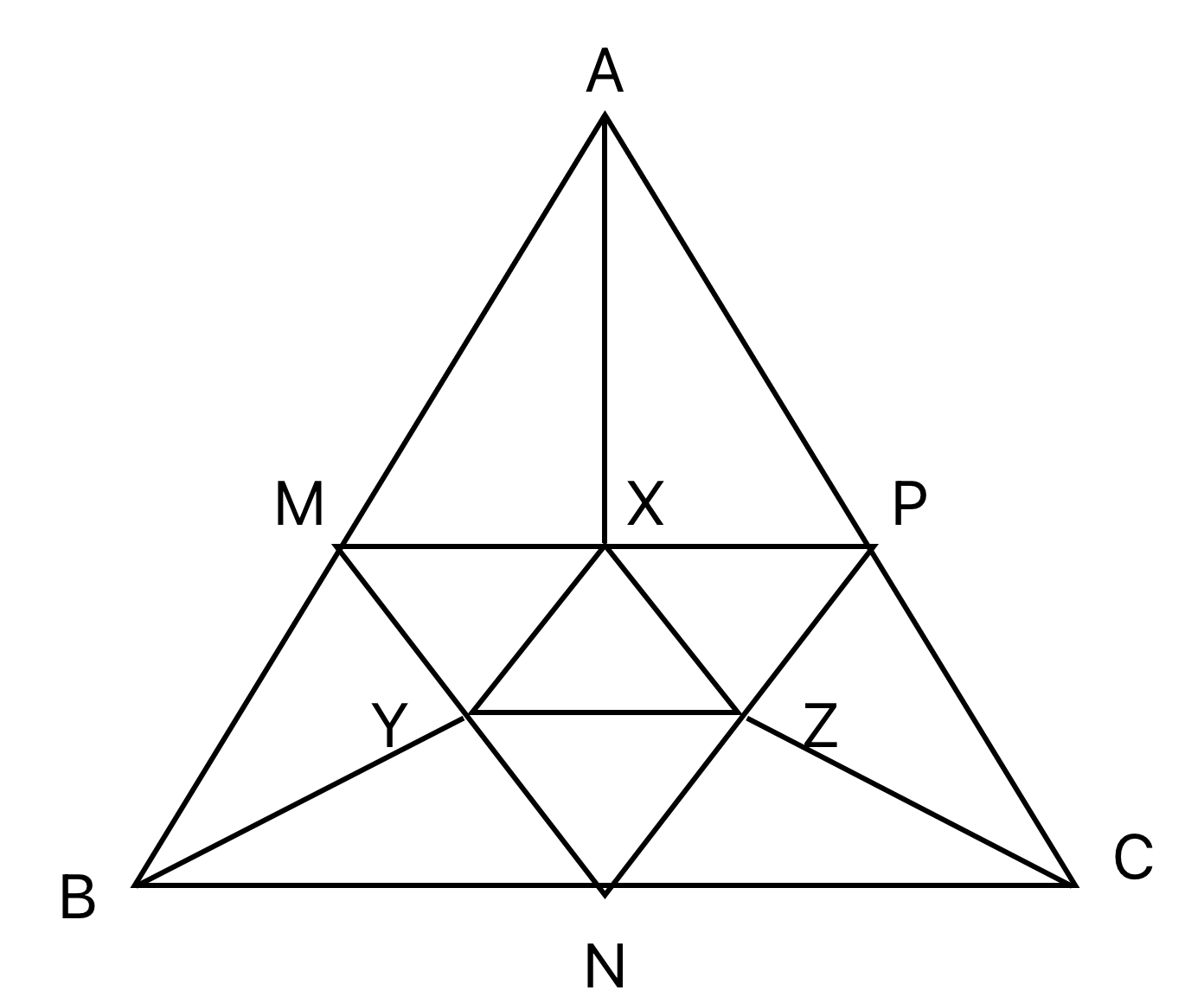
CAT 2024 Slot 3 Quant - Question 66
The midpoints of sides AB, BC, and AC in ΔABC are M, N, and P, respectively. The medians drawn from A, B, and C intersect the line segments MP, MN and NP at X, Y, and Z, respectively. If the area of ΔABC is 1440 sq cm, then the area, in sq cm, of $$\triangle XYZ$$ is
789
456
123
0.-
Clear All
CAT 2024 Slot 3 Quant - Question 67
The number of all positive integers up to 500 with non-repeating digits is
789
456
123
0.-
Clear All
CAT 2024 Slot 3 Quant - Question 68
After two successive increments, Gopal's salary became 187.5% of his initial salary. If the percentage of salary increase in the second increment was twice of that in the first increment, then the percentage of salary increase in the first increment was
Two Factor Authentication
Incase of any issue contact support@cracku.in
CAT Quant Questions | CAT Quantitative Ability
CAT DILR Questions | LRDI Questions For CAT
CAT Verbal Ability Questions | VARC Questions For CAT
Also Read
Frequently Asked Questions
You can download the CAT 2024 Slot 3 Quant Question Paper PDF with detailed answers and solutions from Cracku.
Yes, video solutions are available for every question in the CAT 2024 Slot 3 Quant section to explain step-by-step methods.
The Slot 3 Quant paper covers Arithmetic, Algebra, Geometry, Mensuration, Number Systems, and Modern Math questions.
It helps you practice real exam questions, improve speed and accuracy, and understand the latest exam pattern.
Yes, the solutions explain simple methods, time-saving tricks, and smart approaches to solve Quant questions faster.
Yes, solving the Slot 3 Quant paper with video solutions helps improve accuracy, time management, and overall CAT performance.
.png)