The midpoints of sides AB, BC, and AC in ΔABC are M, N, and P, respectively. The medians drawn from A, B, and C intersect the line segments MP, MN and NP at X, Y, and Z, respectively. If the area of ΔABC is 1440 sq cm, then the area, in sq cm, of $$\triangle XYZ$$ is

The question describes a figure of the following nature, 

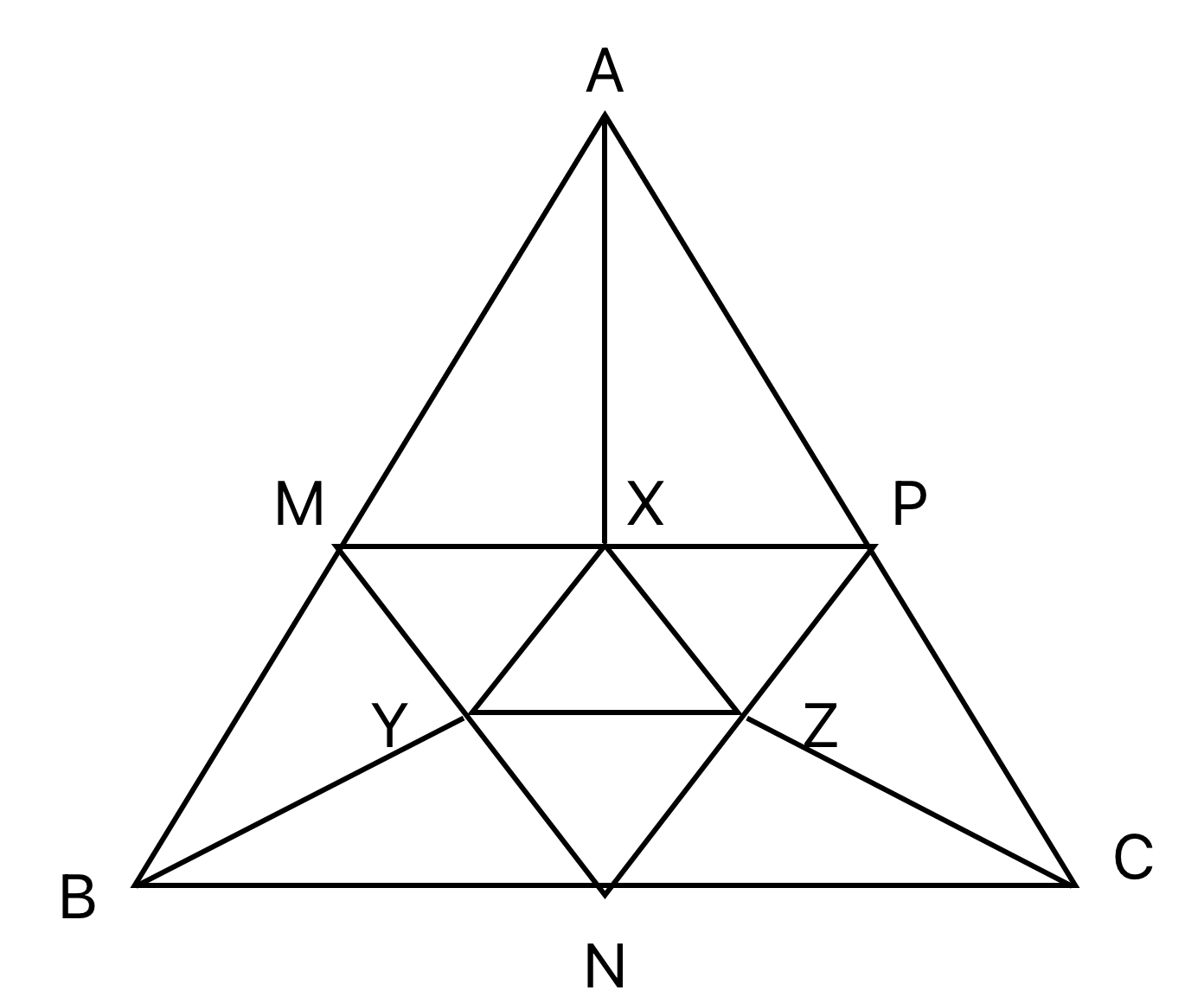
We are told that the area of the triangle ABC is 1440. 
By proportionality theorem, the area of MPN should be one fourth of that. 
Since we know that, $$\frac{\left(Area\ \triangle_1\right)}{Area\ \triangle_2}=\frac{\left(side\ of\ \triangle_1\right)^2}{\left(side\ of\ \triangle_2\right)^2}$$

And since it is given that MPN are midpoints of the respective sides, area of triangle MPN is $$\triangle\ \frac{ABC}{4}=\frac{1440}{4}=360$$

Now, the medians from each side intersect, MP MN and NP are X Y and Z respectively, since these sides are proportional to the main triangle, the point of intersection of the medians with these sides will divide the side MP, MN and NP in half. 

Then, Area of Triangle XYZ will be one fourth the area MPN, 
$$\triangle\ \frac{MPN}{4}=\frac{360}{4}=90$$

The answer is 90.