A circular plot of land is divided into two regions by a chord of length $$10\sqrt{3}$$ meters such that the chord subtends an angle of 120° at the center. Then, the area, in square meters, of the smaller region is

This is the situation that is described in the question above, Angle AOB is 120 degrees and the chord AB is of length 10cm. 

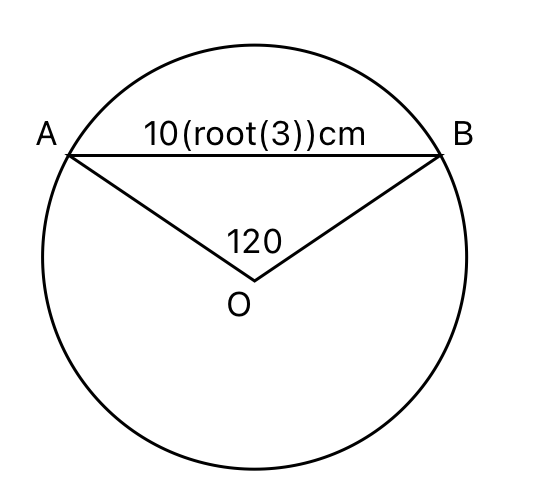
Using Cosine rule we can find the length of AO and AB
$$\cos\left(AOB\right)=\frac{\left(r^2+r^2-300\right)}{2r^2}$$
$$-\frac{1}{2}=\frac{\left(2r^2-300\right)}{2r^2}$$
$$3r^2=300$$
$$r=10$$

Area of the Sector AOB is $$\frac{120}{360}\times\ \pi\ \times\ r^2$$
$$\frac{1}{3}\times\ \pi\ \times\ \frac{100}{1}$$ which is $$\frac{100\pi}{3}\ $$

Area of triangle AOB is $$\frac{1}{2}\times\ r^2\times\ \sin\left(120\right)$$

$$\frac{1}{2}\times\ \frac{100}{1}\times\ \frac{\sqrt{3}}{2}$$

Area of triangle AOB is $$\frac{75}{\sqrt{3}}$$

The smaller region will be, $$\frac{100\pi\ }{3}-\frac{75}{\sqrt{3}}$$
Taking 25 common we will get, 
$$25\left(\cfrac{4 \pi}{3} - \sqrt{3}\right)$$