The number of distinct real values of x, satisfying the equation $$max \left\{x, 2\right\} - min\left\{x, 2\right\} = \mid x + 2 \mid - \mid x - 2 \mid$$, is

The expression on the right-hand side will have two critical points: 2 and -2

For any value of x greater than equal to 2, the equation changes to x+2-(x-2) = 4

the value of min{x,2} would be 2, so we would want max{x,2} to be 4+2 = 6

Therefore, x=6 works. 

For any value of x less than equal to -2, the equation changes to -(x+2)+(x-2) = -4
the value of max{x,2} would be 2, so we would want min{x,2} to be 6 again; this cannot be the case.
In general, subtracting the smaller (min) of the two values from the bigger (max) can not lead to a negative number. The max it can lead to is a 0

When x lies between -2 and 2,  the equation becomes 2x
The maximum function will give back 2, and the minimum function will give back x, with the right-hand side giving 2x
Solving this we would get 2-x = 2x which is x=2/3

Therefore, there are two real values of x for which the given equation holds. 

Hence, 2 is the correct answer.

The graph of the function on the right hand side can be visualised as:

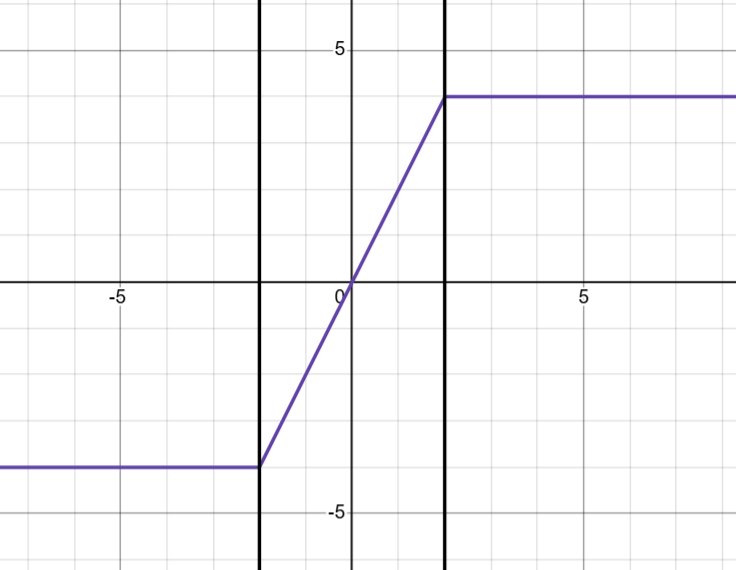
Hence, 2 is the correct answer.