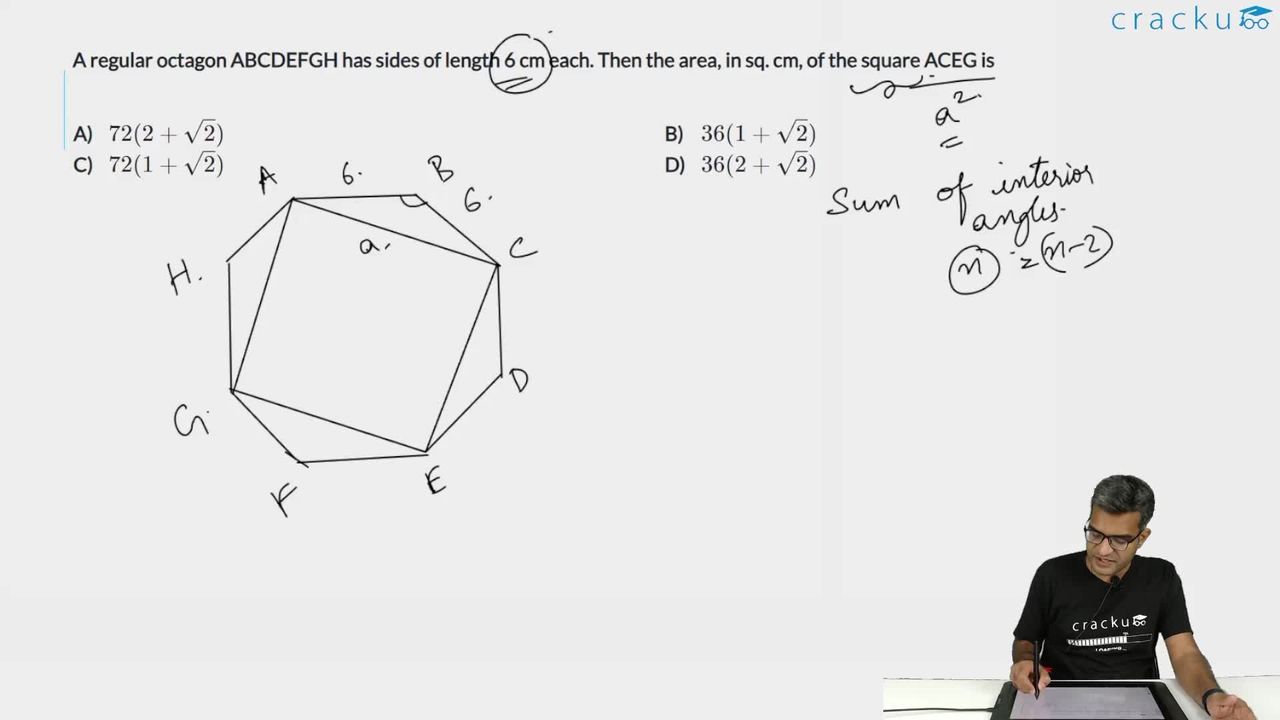
A regular octagon ABCDEFGH has sides of length 6 cm each. Then the area, in sq. cm, of the square ACEG is

This is the figure in the question, 

We are given that each side is 6cm long, 
To find the side AC, we can use cosine rule, since we know each interior angle of the octagon(which is 135 degrees)

$$\cos\left(\angle ABC\right)=\dfrac{\left(AB^2+BC^2-AC^2\right)}{2\left(AB\right)\left(AC\right)}$$

$$\cos\left(135\right)=\dfrac{\left(36+36-AC^2\right)}{2\left(36\right)}$$

$$-\dfrac{1}{\sqrt{2}}=\dfrac{\left(72-AC^2\right)}{72}$$

$$AC^2=72+36\sqrt{2}$$

$$AC^2=36\left(2+\sqrt{2}\right)$$

Since AC is the side of the square, and the area of a square is square of the side. 

Answer is $$36\left(2+\sqrt{2}\right)$$