Top 100 XAT 2026 QADI Questions PDF
Our Top 100 XAT 2026 QADI Questions PDF is an easy-to-use and effective resource to help you improve your Quant and DI preparation for XAT. The QADI section checks your maths basics, logical thinking, calculation skills, and ability to understand data. This PDF covers all important XAT topics—Arithmetic, Algebra, Numbers, Geometry, Modern Math, DI sets, graphs, and tables—so you can practice every major question type.
Each question is created at the actual XAT difficulty level and comes with simple, step-by-step solutions. Whether you are just starting with Quant or aiming for a 99+ percentile, these 100 selected questions will help you improve speed, accuracy, and confidence in the QADI section.
Why Practice with Our Top 100 QADI Questions for XAT 2026?
The XAT Quant & DI section is known for its strong mix of concepts and logical reasoning. Practicing good-quality questions with clear explanations helps you:
-
Strengthen your basics in all major Quant topics
-
Increase your problem-solving speed and reduce calculation mistakes
-
Learn how to solve tricky DI sets more effectively
-
Understand the exact style of XAT questions
-
Feel confident while solving medium to tough questions in the exam
With the XAT 2026 QADI PDF, you can revise better, avoid common errors, and steadily improve your performance—helping you score well in one of the most important sections of the exam.
List of XAT QADI Questions
Question 1
A manufacturer produces two types of products - A and B, which are subjected to two types of operations, viz. grinding and polishing. Each unit of product A takes 2 hours of grinding and 3 hours of polishing whereas product B takes 3 hours of grinding and 2 hours of polishing. The manufacturer has 10 grinders and 15 polishers. Each grinder operates for 12 hours/day and each polisher 10 hours/day. The profit margin per unit of A and B are Rs. 5/ - and Rs. 7/ - respectively. If the manufacturer utilises all his resources for producing these two types of items, what is the maximum profit that the manufacturer can earn in a day?
correct answer:- 2
Question 2
Rani bought more apples than oranges. She sells apples at Rs. 23 apiece and makes 15% profit. She sells oranges at Rs. 10 a piece and makes 25% profit. If she gets Rs. 653 after selling all the apples and oranges, find her profit percentage.
correct answer:- 2
Question 3
The Maximum Retail Price (MRP) of a product is 55% above its manufacturing cost. The product is sold through a retailer, who earns 23% profit on his purchase price. What is the profit percentage (expressed in nearest integer) for the manufacturer who sells his product to the retailer? The retailer gives 10% discount on MRP.
correct answer:- 4
Question 4
Nikhil’s mother asks him to buy 100 pieces of sweets worth 100/-. The sweet shop has 3 kinds of sweets, kajubarfi, gulabjamun and sandesh. Kajubarfi costs 10/- per piece, gulabjamun costs 3/- per piece and sandesh costs 50 paise per piece. If Nikhil decides to buy at least one sweet of each type, how many gulabjamuns should he buy?
correct answer:- 1
Question 5
If $$\log_4m + \log_4n = \log_2(m + n)$$ where m and n are positive real numbers, then which of the following must be true?
correct answer:- 5
Question 6
Consider the equation $$\log_5(x - 2) = 2 \log_{25}(2x - 4)$$, where x is a real number.
For how many different values of x does the given equation hold?
correct answer:- 1
Question 7
For how many distinct real values of $$x$$ does the equation below hold true? (Consider $$a$$ > 0.)
$$\dfrac{x^2 \log_a(16)}{\log_a(32)} - \dfrac{\log_a(64)}{\log_a(32)} - x = 0 $$
correct answer:- 5
Question 8
Consider the formula, $$S=\frac{\alpha\times\omega}{\tau+\rho\times\omega}$$ positive integers. If ⍵ is increased and ⍺, τ and ρ are kept constant, then S:
correct answer:- 1
Question 9
Prof. Suman takes a number of quizzes for a course. All the quizzes are out of 100. A student can get an A grade in the course if the average of her scores is more than or equal to 90.Grade B is awarded to a student if the average of her scores is between 87 and 89 (both included). If the average is below 87, the student gets a C grade. Ramesh is preparing for the last quiz and he realizes that he will score a minimum of 97 to get an A grade. After the quiz, he realizes that he will score 70, and he will just manage a B. How many quizzes did Prof. Suman take?
correct answer:- 4
Question 10
A teacher noticed a strange distribution of marks in the exam. There were only three distinct
scores: 6, 8 and 20. The mode of the distribution was 8. The sum of the scores of all the students was 504. The number of students in the in most populated category was equal to the sum of the number of students with lowest score and twice the number of students with the highest score. The total number of students in the class was:
correct answer:- 5
Question 11
Ramesh analysed the monthly salary figures of five vice presidents of his company. All the salary figures are integers. The mean and the median salary figures are 5 lakh, and the only mode is 8 lakh. Which of the options below is the sum (in lakh) of the highest and the lowest salaries?
correct answer:- 1
Question 12
A computer program was tested 300 times before its release. The testing was done in three stages
of 100 tests each. The software failed 15 times in Stage I, 12 times in Stage II, 8 times in Stage III, 6 times in both Stage I and Stage II, 7 times in both Stage II and Stage III, 4 times in both Stage I and Stage III, and 4 times in all the three stages. How many times the software failed in a single stage only?
correct answer:- 2
Question 13
A boat, stationed at the North of a lighthouse, is making an angle of 30° with the top of the lighthouse. Simultaneously, another boat, stationed at the East of the same lighthouse, is making an angle of 45° with the top of the lighthouse. What will be the shortest distance between these two boats? The height of the lighthouse is 300 feet. Assume both the boats are of negligible dimensions.
correct answer:- 4
Question 14
A girl travels along a straight line, from point A to B at a constant speed, $$V_1$$ meters/sec for T seconds. Next, she travels from point B to C along a straight line, at a constant speed of $$V_2$$ meters/sec for another T seconds. BC makes an angle 105° with AB. If CA makes an angle 30° with BC, how much time will she take to travel back from point C to A at a constant speed of $$V_2$$ meters/sec, if she travels along a straight line from C to A?
correct answer:- 3
Question 15
Two friends, Ram and Shyam, start at the same point, at the same time. Ram travels straight north at a speed of 10km/hr, while Shyam travels straight east at twice the speed of Ram. After 15 minutes, Shyam messages Ram that he is just passing by a large telephone tower and after another 15 minutes Ram messages Shyam that he is just passing by an old banyan tree. After some more time has elapsed, Ram and Shyam stop. They stop at the same point of time. If the straight-line distance between Ram and Shyam now is 50 km, how far is Shyam from the banyan tree (in km)? (Assume that Ram and Shyam travel on a flat surface.)
correct answer:- 1
Question 16
A hare and a tortoise run between points O and P located exactly 6 km from each other on a straight line. They start together at O, go straight to P and then return to O along the same line. They run at constant speeds of 12 km/hr and 1 km/hr respectively. Since the tortoise is slower than the hare, the hare shuttles between O and P until the tortoise goes once to P and returns to O. During the run, how many times are the hare and the tortoise separated by an exact distance of 1 km from each other?
correct answer:- 5
Question 17
At any point of time, let x be the smaller of the two angles made by the hour hand with the minute hand on an analogue clock (in degrees). During the time interval from 2:30 p.m. to 3:00 p.m., what is the minimum possible value of x?
correct answer:- 3
Question 18
Let ABC be an isosceles triangle. Suppose that the sides AB and AC are equal and let the length of AB be x cm. Let b denote the angle ∠ABC and sin b = 3/5. If the area of the triangle ABC is M square cm, then which of the following is true about M?
correct answer:- 5
Question 19
Rajesh, a courier delivery agent, starts at point A and makes a delivery each at points B, C and D, in that order. He travels in a straight line between any two consecutive points. The following are known: (i) AB and CD intersect at a right angle at E, and (ii) BC, CE and ED are respectively 1.3 km, 0.5 km and 2.5 km long. If AD is parallel to BC, then what is the total distance (in km) that Rajesh covers in travelling from A to D?
correct answer:- 3
Question 20
The six faces of a wooden cube of side 6 cm are labelled A, B, C, D, E and F respectively. Three of these faces A, B, and C are each adjacent to the other two, and are painted red. The other three faces are not painted. Then, the wooden cube is neatly cut into 216 little cubes of equal size. How many of the little cubes have no sides painted?
correct answer:- 1
Question 21
ABC is a triangle with integer-valued sides AB = 1, BC >1, and CA >1. If D is the mid-point of AB, then, which of the following options is the closest to the maximum possible value of the angle ACD (in degrees)?
correct answer:- 1
Question 22
The topmost point of a perfectly vertical pole is marked A. The pole stands on a flat ground at point D. The points B and C are somewhere between A and D on the pole. From a point E, located on the ground at a certain distance from D, the points A, B and C are at angles of 60, 45 and 30 degrees respectively. What is AB : BC : CD?
correct answer:- 4
Question 23
Two circles P and Q, each of radius 2 cm, pass through each other’s centres. They intersect at points A and B. A circle R is drawn with diameter AB. What is the area of overlap (in square cm) between the circles R and P?
correct answer:- 5
Question 24
Find the value of
$$\frac{\sin^{6}15^{\circ} + \sin^{6}75^{\circ} + 6\sin^{2}15^{\circ}\sin^{2}75^{\circ}}{\sin^{4}15^{\circ} + \sin^{4}75^{\circ} + 5\sin^{2}15^{\circ}\sin^{2}75^{\circ}}$$
correct answer:- 3
Question 25
ABC is a triangle with BC=5. D is the foot of the perpendicular from A on BC. E is a point on CD such that BE=3. The value of $$AB^2 - AE^2 + 6CD$$ is:
correct answer:- 5
Question 26
ABC is a triangle and the coordinates of A, B and C are (a, b-2c), (a, b+4c) and (-2a,3c) respectively where a, b and c are positive numbers.
The area of the triangle ABC is:
correct answer:- 4
Question 27
A non-flying ant wants to travel from the bottom corner to the diagonally opposite top corner of a cubical room. The side of the room is 2 meters. What will be the minimum distance that the ant needs to travel?
correct answer:- 5
Question 28
ABCD is a trapezoid where BC is parallel to AD and perpendicular to AB. Kindly note that BC< AD. P is a point on AD such that CPD is an equilateral triangle. Q is a point on BC such that AQ is parallel to PC. If the area of the triangle CPD is $$4\sqrt{\ 3}$$, find the area of the triangle ABQ.
correct answer:- 1
Question 29
ABCD is a trapezoid where BC is parallel to AD and perpendicular to AB. Kindly note that BC< AD. P is a point on AD such that CPD is an equilateral triangle. Q is a point on BC such that AQ is parallel to PC. If the area of the triangle CPD is $$4\sqrt{\ 3}$$, find the area of the triangle ABQ.
correct answer:- 1
Go through the information given below, and answer the THREE questions that follow.Comprehension:The three graphs below capture relationship between economic (and social) activities and subjective well-being. The first graph (Graph-1) captures relationship between GDP (percapita) and Satisfaction with life, across different countries and four islands: Gizo, Roviana, Niijhum Dwip, and Chittagong. The Graph-2 captures three different measures of subjective well-being (Satisfaction with life, Affect Balance and Momentary Affect) across the four islands, which have different levels monetization (Index). The Graph-3 captures levels of thirteen different socio-economic activities across four islands.
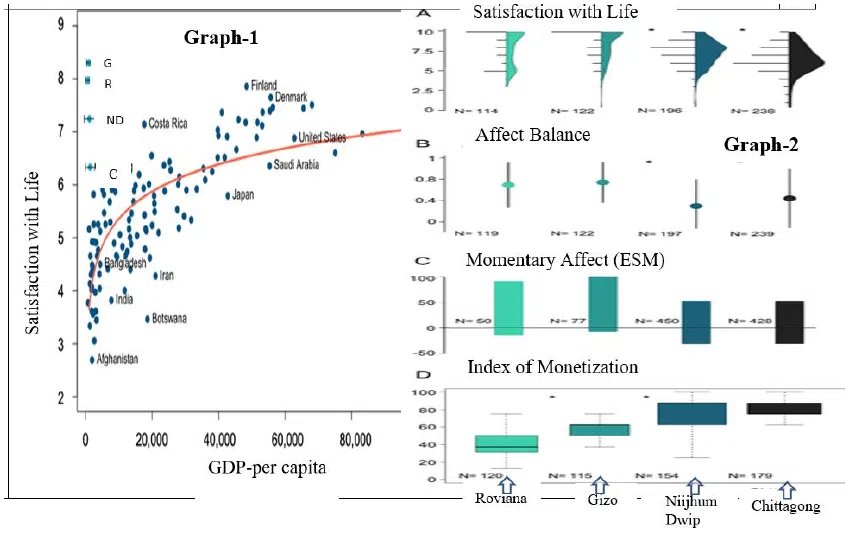
Question 30
Which of the following will BEST capture the relationship between GDP (x-axis) and Life Satisfaction (y-axis) of countries?
correct answer:- 3
Question 31
The _____ refers to investments made for product development, marketing, and market research.
correct answer:- 2
Question 32
An investor lent-out a certain sum on simple interest and the same sum on compound interest at the same rate of interest per annum. He noticed that the ratio of the difference of the compound interest and the simple interest for 4 years to the difference of the compound interest and the simple interest for 3 years is 20:8. The approximate rate of interest per annum is given by,
correct answer:- 1
:Read the following Passage and Answer the questions given below:
You absolutely must develop feelings of self-esteem and confidence to become empowered. No amount of willpower can surmount the feeling of defeatism. Any negative thoughts will filter into your subconscious mind, which does not question or analyze the data it receives. If you have experienced repeated failure in past attempts to change a behavior pattern, your total self-image becomes established and fixed as one of failure. You become so convinced that you are incapable of reversing this trend that you eventually stop picturing a desirable goal for yourself. You resign yourself to accepting the current situation as being permanent and helpless.
A positive self-image must be fed into your subconscious mind without being evaluated by the critical factor of your conscious mind proper (defense mechanisms). The most efficient and effective method of accomplishing this goal is by practicing self-hypnosis.
Although many obstacles may arise during your consciousness raising program, the proper use of self-programming will transform these former roadblocks into stepping-stones of success. Once you envision succeeding in your goals, former difficulties disappear, and the subconscious becomes your chief ally in strengthening your ability to meet challenges.
The subconscious mind contains all memories. It is a natural computer and is continually being programmed with data originating from the conscious mind proper. The subconscious cannot alter this data; however~ it does direct the conscious mind to act in a specific way. The conscious mind is always resistant to change, any change, even if it is for the better. The conscious mind likes business as usual. Consciousness raising and behavioral changes are not business as usual; therefore, the conscious mind is your only enemy.
By seeing yourself as you desire to be, you are reprogramming your subconscious computer. This does not require a critical acceptance, because your subconscious is incapable of analytical thought. Accompanying this visualization will be a feeling that you have already attained this goal. This as-if approach is remarkably successful.
Once you achieve a particular goal using the subconscious mind~ the maintenance of this goal will be effortless. When something attempts to interfere with the proper functioning of the reprogrammed subconscious, your internal computer will recognize the error immediately, and it will be corrected by this feedback mechanism.
Your initial efforts in reprogramming the subconscious require a certain amount of mental training, which encompasses all new goals and aspirations. Daily practice of the exercises self-hypnosis, yoga~ hetero-hypnosis, and trance results in a permanent reprogramming of the subconscious computer and a spontaneous incorporation of this goal. Willpower is neither necessary nor desirable for this paradigm. This is one example of raising consciousness.
Your imagination can create a new mental image of yourself. If you have properly implanted the subconscious with positive images and suggestions, you automatically alter your behavior to act in accordance with this new programming. A new sense of well-being and accomplishment accompany this pattern of behavior. You will be able to feel this sense of confidence and empowerment for prolonged periods following additional practice sessions.
Willpower alone cannot result in permanent changes in behavior. The problem with the willpower approach is that you are consciously placing too much emphasis on past failures. As a result, your mental mindset is not conducive to improvement, and subsequent efforts prove only more frustrating. Success in applying consciousness-raising techniques depends on the subconscious mind's uncritical acceptance of constructive suggestions. Thus, the most effective method of achieving this is through the use of self-hypnosis.
Question 33
According to the passage, the subconscious mind .... :
correct answer:- 3
Read the following Passage and Answer the questions given below:
Widespread currency manipulation, mainly in developing and newly industrialized economies, is the most important development of the past decade in international financial markets. In an attempt to hold-down the values of their currencies, governments are distorting capital flows by around $1.5 trillion per year. The result is a net drain on aggregate demand in the United States and the Euro area by an amount roughly equal to the large output gaps in the United States and the Euro area. In other words, millions more Americans and Europeans would be employed if other countries did not manipulate their currencies and instead achieved sustainable growth through higher domestic demand.
The United States has lost 1 million to 5 million jobs due to this foreign currency manipulation. More than 20 countries have increased their aggregate foreign exchange reserves and other official foreign assets by an annual average of nearly $1. 5 trillion in recent years. This build-up of official assets-mainly through intervention in the foreign exchange markets; keeps the currencies of the interveners substantially undervalued, thus boosting their international competitiveness and trade surpluses. The corresponding trade deficits are spread around the world, but the largest share of the loss centers on the United States, whose trade deficit has increased by $200 billion to $500 billion per year as a result.
The United States must tighten fiscal policy over the coming decade to bring its national debt under control. Monetary policy has already exhausted most of its expansionary potential. Hence the United States must eliminate or at least sharply reduce its large trade deficit to accelerate growth and restore full employment. The way to do so, at no cost to the US budget, is to insist that other countries stop manipulating their currencies and permit the dollar to regain a competitive level. This can be done through steps fully consistent with the international obligations of the United States that are indeed based on existing International Monetary Fund (IMF) guidelines.
Such a strategy should in fact attract considerable support from other countries that are adversely affected b the manipulation, including Australia, Canada, the euro area, Brazil, India, Mexico, and a number of other developing economies. The strategy would aim to fill a major gap in the existing international financial architecture: its inability to engage surplus countries, even when they blatantly violate the legal strictures against competitive currency undervaluation, in an equitable sharing of global rebalancing requirements.
The United States and its allies should first seek voluntary agreement from the manipulators to sharply reduce or eliminate their intervention. The United States should inform the manipulators that if they do not do so, the United States will adopt four new policy measures against their currency activities. First, it will undertake countervailing currency intervention (CCI) against countries with convertible currencies by buying amounts of their currencies equal to the amounts of dollars they are buying themselves, to neutralize the impact on exchange rates. Second, it will tax the earnings on, or restrict further purchases of, dollar assets acquired by intervening countries with inconvertible currencies (where CCI could therefore not be fully effective to penalize them for building up these positions. Third, it will hereafter treat manipulated exchange rates as export subsidies for purposes of levying countervailing import duties. Fourth, hopefully with a number of other adversely affected countries, it will bring a case against the manipulators in the World Trade Organization (WTO) that would authorize more wide-ranging trade retaliation.
Question 34
The term "currency manipulation" by the developing and newly industrialized economies a mentioned in the pa sage can be explained as ..............
correct answer:- 2
Question 35
A number is interesting if on adding the sum of the digits of the number and the product of the digits of the number, the result is equal to the number. What fraction of numbers between 10 and 100 (both 10 and 100 included) is interesting?
correct answer:- 5
Question 36
p and q are positive numbers such that $$p^q = q^p$$, and $$q = 9p$$. The value of p is
correct answer:- 4
Question 37
Consider the expression $$(xxx)_{b}=x^3$$, where b is the base, and x is any digit of base b. Find the value of b:
correct answer:- 5
Question 38
Please read the following sentences carefully:
I — 103 and 7 are the only prime factors of 1000027
II — $$\sqrt[6]{6!}>\sqrt[7]{7!}$$
III — If I travel one half of my journey at an average speed of x km/h, it will be impossible for me to attain an average speed of 2x km/h for the entire journey.
correct answer:- 3
Question 39
If $$N = (11^{p + 7})(7^{q - 2})(5^{r + 1})(3^{s})$$ is a perfect cube, where $$p, q, r$$ and $$s$$ are positive integers, then the smallest value of $$p + q + r + s$$ is :
correct answer:- 5
Question 40
A three - digit number has digits in strictly descending order and divisible by 10. By changing the places of the digits a new three - digit number is constructed in such a way that the new number is divisible by 10. The difference between the original number and the new number is divisible by 40. How many numbers will satisfy all these conditions?
correct answer:- 2
Question 41
If the last 6 digits of [(M)! - (N)!] are 999000, which of the following option is not possible for (M) × (M - N)? Both (M) and (N) are positive integers and M > N. (M)! is factorial M.
correct answer:- 2
Question 42
$$x, 17, 3x - y^{2} - 2$$, and $$3x + y^{2} - 30$$, are four consecutive terms of an increasing arithmetic sequence. The sum of the four number is divisible by:
correct answer:- 1
Question 43
Two numbers, $$297_{B}$$ and $$792_{B}$$ , belong to base B number system. If the first number is a factor of the second number then the value of B is:
correct answer:- 5
Question 44
Read the following instruction carefully and answer the question that follows:
Expression $$\sum_{n=1}^{13}\frac{1}{n}$$ can also be written as $$\frac{x}{13!}$$ What would be the remainder if x is divided by 11?
correct answer:- 4
Question 45
Consider four natural numbers: x, y, x + y, and x - y. Two statements are provided below:
I. All four numbers are prime numbers.
II. The arithmetic mean of the numbers is greater than 4.
Which of the following statements would be sufficient to determine the sum of the four numbers?
correct answer:- 1
Based on the following information.
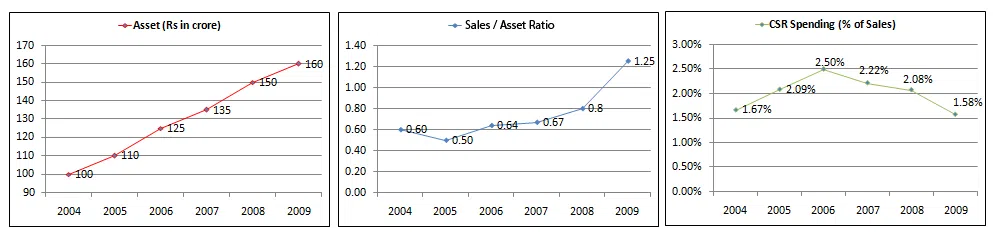
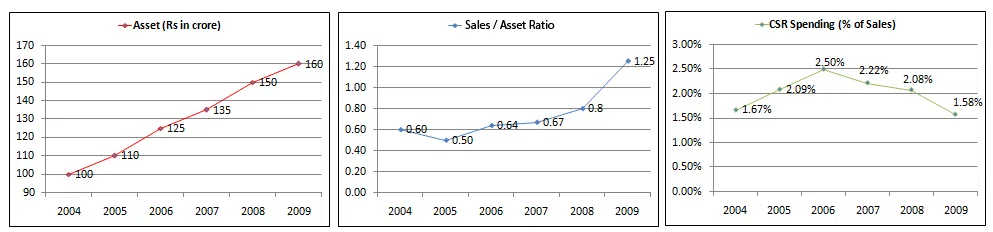
The following graphs give annual data of Assets, Sales (as percentage of Assets) and Spending on Corporate Social Responsibility (CSR) (as percentage of Sales), of a company for the period 2004 - 2009.
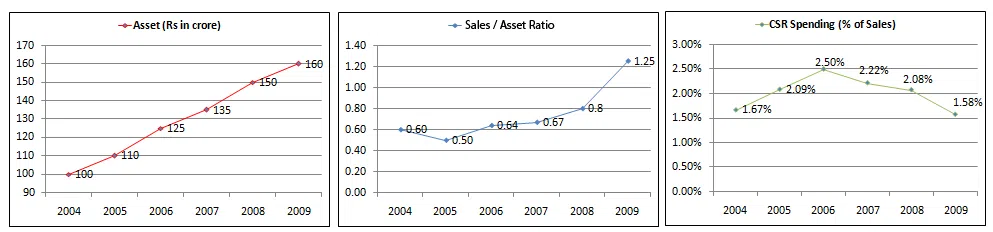
Question 46
In which year was the increase in spending on CSR, vis - à - vis the previous year, the maximum?
correct answer:- 2
Based on the following information.
The following graphs give annual data of Assets, Sales (as percentage of Assets) and Spending on Corporate Social Responsibility (CSR) (as percentage of Sales), of a company for the period 2004 - 2009.
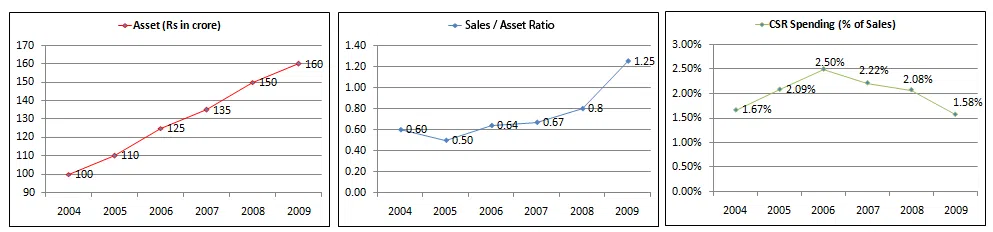
Question 47
Of the years indicated below, in which year was the ratio of CSR/ Assets the maximum?
correct answer:- 5
Based on the following information.
The following graphs give annual data of Assets, Sales (as percentage of Assets) and Spending on Corporate Social Responsibility (CSR) (as percentage of Sales), of a company for the period 2004 - 2009.
Question 48
The maximum value of spending on CSR activities in the period 2004-2009 is closest to which of the following options?
correct answer:- 4
Based on the following information.
The following graphs give annual data of Assets, Sales (as percentage of Assets) and Spending on Corporate Social Responsibility (CSR) (as percentage of Sales), of a company for the period 2004 - 2009.
Question 49
In which year, did the spending on CSR (measured in Rs) decline, as compared to previous year?
correct answer:- 5
Based on the following information.
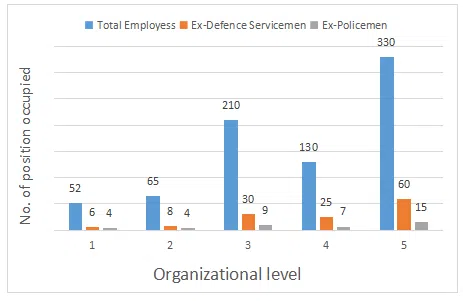
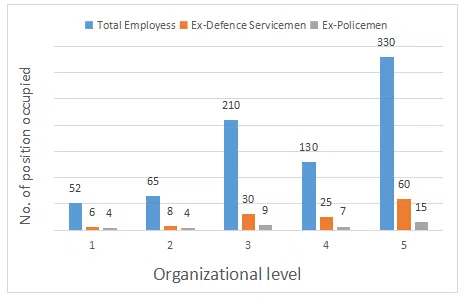
Five years ago Maxam Glass Co. had estimated its staff requirements in the five levels in their organization as: Level - 1: 55; Level - 2: 65; Level - 3: 225 ; Level - 4: 255 & Level - 5: 300. Over the years the company had recruited people based on ad-hoc requirements, in the process also selecting ex-defence service men and ex -policemen. The following graph shows actual staff strength at various levels as on date.
Question 50
The level in which the Ex-Defence Servicemen are highest in percentage terms is:
correct answer:- 4
Based on the following information.
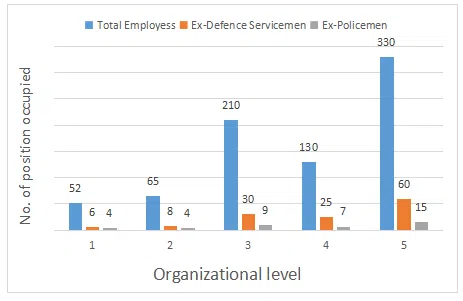
Five years ago Maxam Glass Co. had estimated its staff requirements in the five levels in their organization as: Level - 1: 55; Level - 2: 65; Level - 3: 225 ; Level - 4: 255 & Level - 5: 300. Over the years the company had recruited people based on ad-hoc requirements, in the process also selecting ex-defence service men and ex -policemen. The following graph shows actual staff strength at various levels as on date.
Question 51
If the company decides to abolish all vacant posts at all levels, which level would incur the highest reduction in percentage terms ?
correct answer:- 4
Based on the following information.
Five years ago Maxam Glass Co. had estimated its staff requirements in the five levels in their organization as: Level - 1: 55; Level - 2: 65; Level - 3: 225 ; Level - 4: 255 & Level - 5: 300. Over the years the company had recruited people based on ad-hoc requirements, in the process also selecting ex-defence service men and ex -policemen. The following graph shows actual staff strength at various levels as on date.
Question 52
Among all levels, which level has the lowest representation of Ex- policemen?
correct answer:- 3
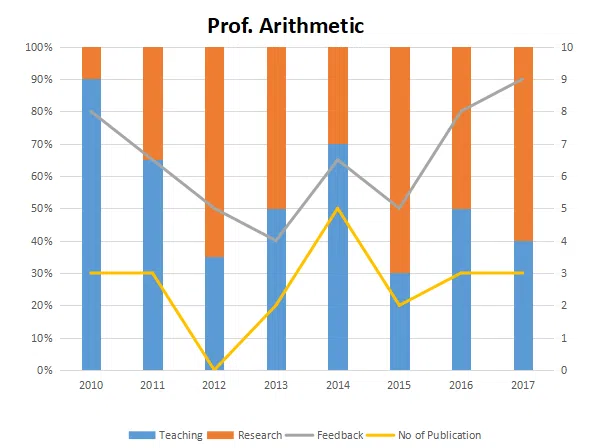
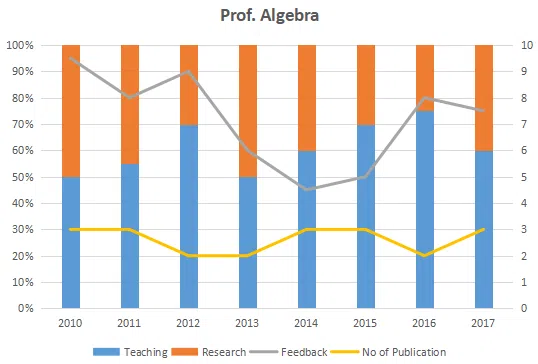
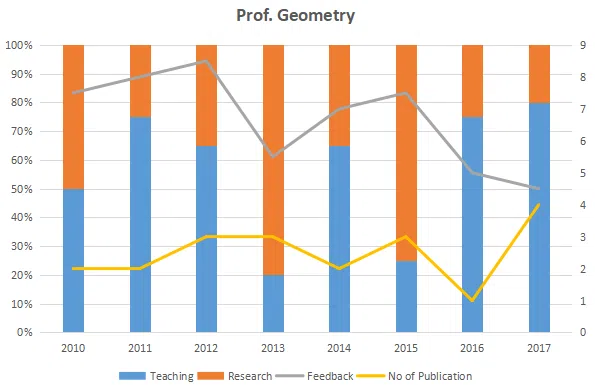
The graph below represent the performance of four professors, across years. measured on four variables: Percentage of time spent on research, teaching, feedback on (a scale of 10. right-hand side) and number of publications (right-hand side). Assume that the cumulative time spent per year on research and teaching activities are sane for all four professors and each of them taught only one course of 90 classroom hours.
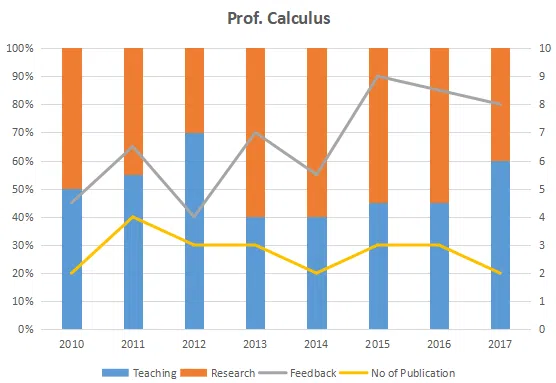
Question 53
Which of the following, shows the maximum year to year percentage growth in feedback?
correct answer:- 3
The graph below represent the performance of four professors, across years. measured on four variables: Percentage of time spent on research, teaching, feedback on (a scale of 10. right-hand side) and number of publications (right-hand side). Assume that the cumulative time spent per year on research and teaching activities are sane for all four professors and each of them taught only one course of 90 classroom hours.
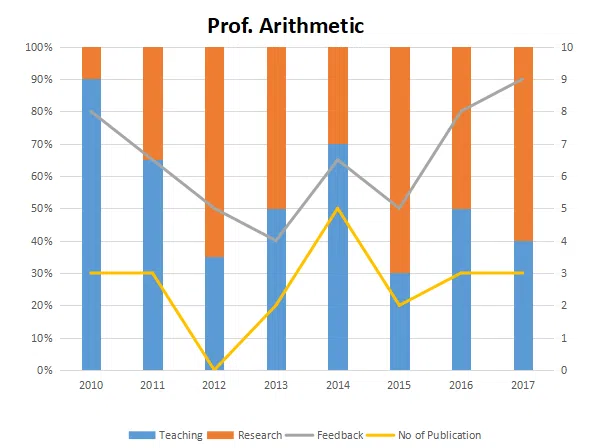
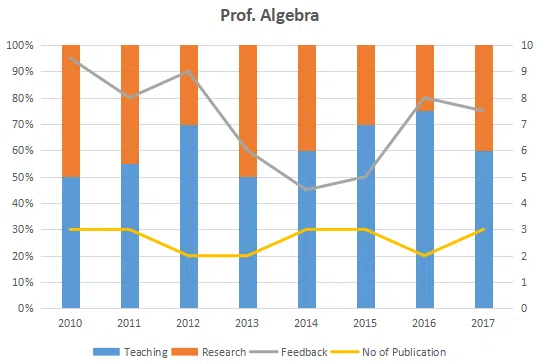
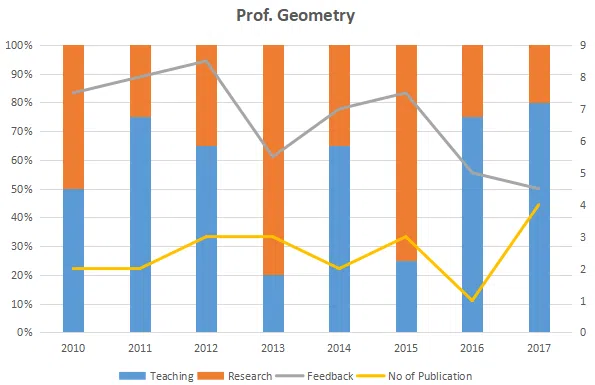
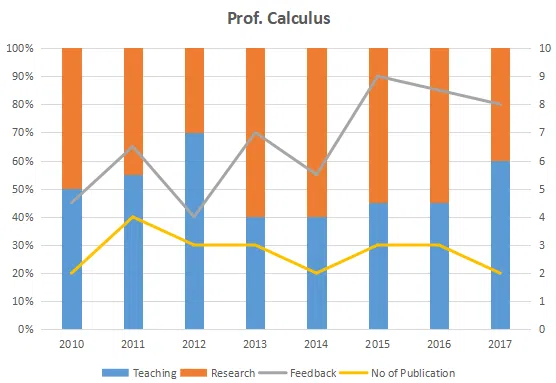
Question 54
Count the number of instances in which "annual decreasing efforts in research" is accompanied with "annual increase in feedback"?
correct answer:- 3
The graph below represent the performance of four professors, across years. measured on four variables: Percentage of time spent on research, teaching, feedback on (a scale of 10. right-hand side) and number of publications (right-hand side). Assume that the cumulative time spent per year on research and teaching activities are sane for all four professors and each of them taught only one course of 90 classroom hours.
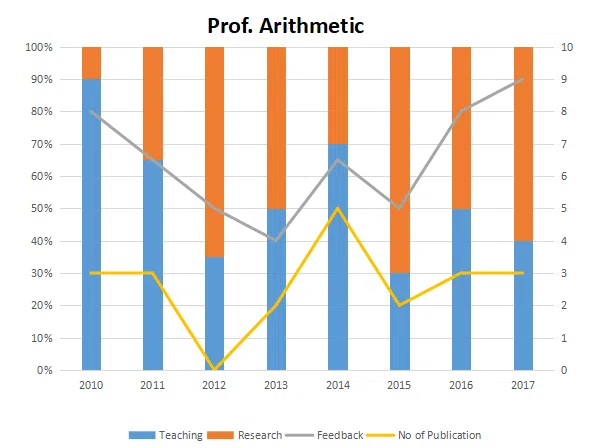
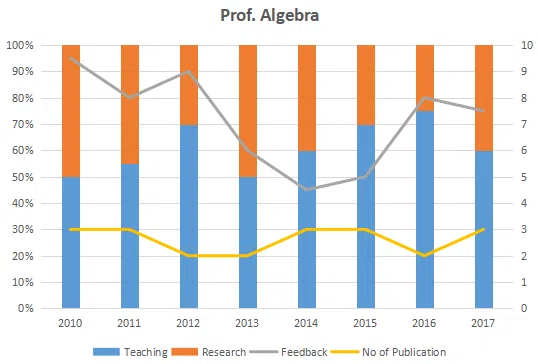
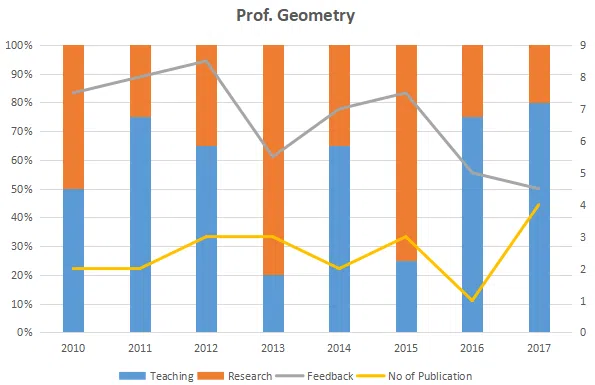
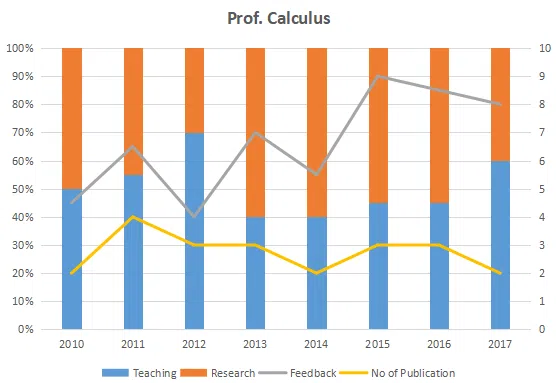
Question 55
Research efficiency is the ratio of cumulative number of publication for a period of 3 years to the cumulative number of hours spent on research activity in those 3 years. Which of the following professors is the least efficient researcher for the period 2015 to 2017?
correct answer:- 1
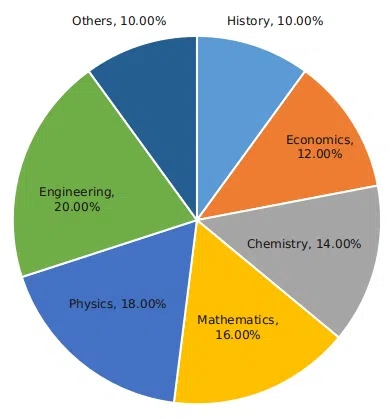
The break-up of the students in a university by subject major is given in the polar pie-chart. The bar chart shows the number of students who major in physics by geographic location.
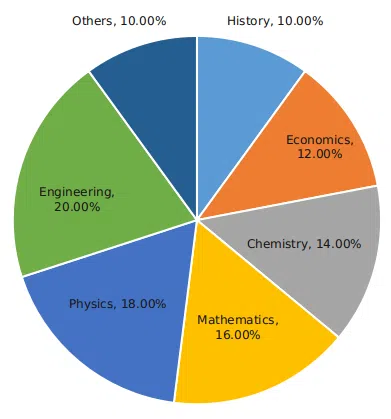
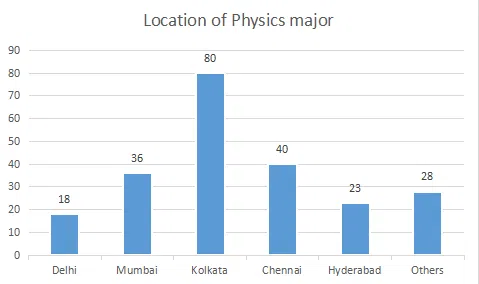
Question 56
How many students major in chemistry?
correct answer:- 2
The break-up of the students in a university by subject major is given in the polar pie-chart. The bar chart shows the number of students who major in physics by geographic location.
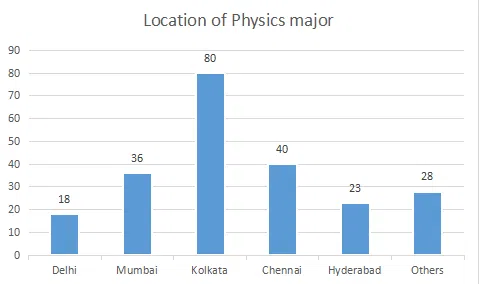
Question 57
If the proportion of physics majors who are from Delhi is the same as the proportion of engineering majors who are from Delhi, how many engineering majors are from Delhi?
correct answer:- 4
The break-up of the students in a university by subject major is given in the polar pie-chart. The bar chart shows the number of students who major in physics by geographic location.
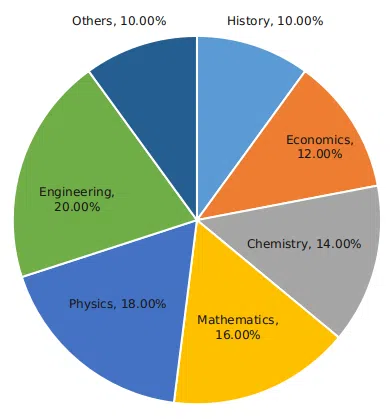
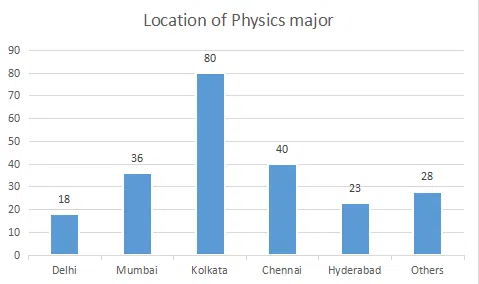
Question 58
12% of all students are from Chennai. What is the largest possible percentage of economics students that can be from Chennai, rounded off to the nearest integer?
correct answer:- 1
Read the information given below and answer the 3 associated questions.
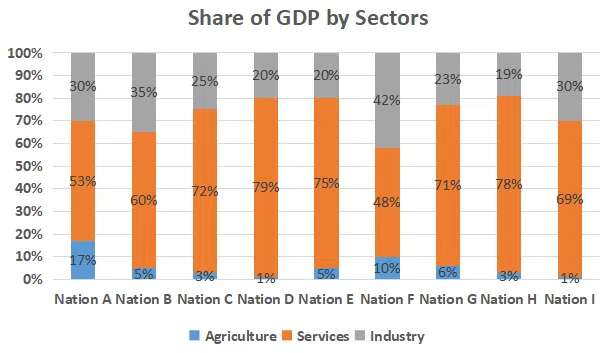
The following graph depicts sector-wise percentage contributions to the gross domestic product (GDP) of nine nations, labelled “Nation A”, “Nation B” and so on. It is known that these nations are Brazil, China, France, Germany, India, Japan, Russia, the UK and the USA, but not necessarily in the same order.
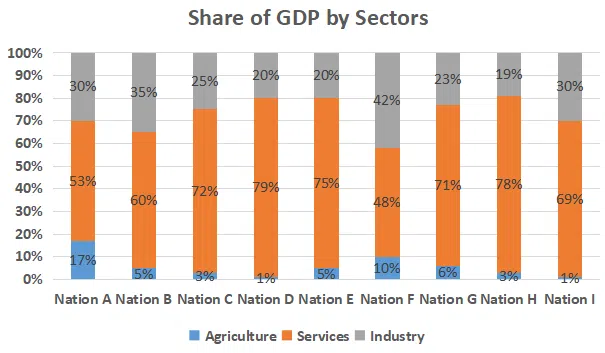
The following, however, are known:
i) The GDPs of the nine nations (in US $ trillion) are:

ii) China has the highest agriculture sector GDP, valued at US $1 trillion, followed respectively by the USA and India
iii) In terms of percentage contribution to the respective nations’ GDPs by their service sectors, the UK and France are respectively the first and the second
iv) Nation A, Nation B and Nation G have the same GDP
v) The GDP of India’s industry sector is lower than the GDP of Russia’s industry sector. However,it is larger than that of Brazil's industry sector
Question 59
Based on the given information, how many nations can be uniquely identified?
correct answer:- 1
Read the information given below and answer the 3 associated questions.
The following graph depicts sector-wise percentage contributions to the gross domestic product (GDP) of nine nations, labelled “Nation A”, “Nation B” and so on. It is known that these nations are Brazil, China, France, Germany, India, Japan, Russia, the UK and the USA, but not necessarily in the same order.
The following, however, are known:
i) The GDPs of the nine nations (in US $ trillion) are:

ii) China has the highest agriculture sector GDP, valued at US $1 trillion, followed respectively by the USA and India
iii) In terms of percentage contribution to the respective nations’ GDPs by their service sectors, the UK and France are respectively the first and the second
iv) Nation A, Nation B and Nation G have the same GDP
v) The GDP of India’s industry sector is lower than the GDP of Russia’s industry sector. However,it is larger than that of Brazil's industry sector
Question 60
Based on the given information, which of the following CANNOT be ruled out?
correct answer:- 4
Read the information given below and answer the 3 associated questions.
The following graph depicts sector-wise percentage contributions to the gross domestic product (GDP) of nine nations, labelled “Nation A”, “Nation B” and so on. It is known that these nations are Brazil, China, France, Germany, India, Japan, Russia, the UK and the USA, but not necessarily in the same order.
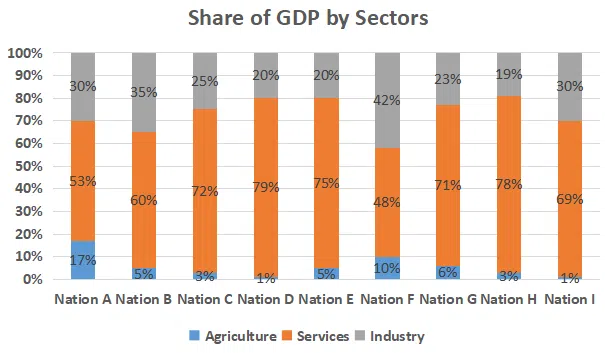
The following, however, are known:
i) The GDPs of the nine nations (in US $ trillion) are:

ii) China has the highest agriculture sector GDP, valued at US $1 trillion, followed respectively by the USA and India
iii) In terms of percentage contribution to the respective nations’ GDPs by their service sectors, the UK and France are respectively the first and the second
iv) Nation A, Nation B and Nation G have the same GDP
v) The GDP of India’s industry sector is lower than the GDP of Russia’s industry sector. However,it is larger than that of Brazil's industry sector
Question 61
Which of the following information, when considered in addition to the given information, does not allow us to completely identify the nine nations in the graph?
correct answer:- 1
Question 62
Given $$A = |x + 3| + | x - 2 | - | 2x -8|$$. The maximum value of $$|A|$$ is:
correct answer:- 2
Question 63
In a school, the number of students in each class, from Class I to X, in that order, are in an arithmetic progression. The total number of students from Class I to V is twice the total number of students from Class VI to X.
If the total number of students from Class I to IV is 462, how many students are there in Class VI?
correct answer:- 4
Question 64
Let $$f(x) = \frac{x^2 + 1}{x^2 - 1}$$ if $$x \neq 1, -1,$$ and 1 if x = 1, -1. Let $$g(x) = \frac{x + 1}{x - 1}$$ if $$x \neq 1,$$ and 3 if x = 1.
What is the minimum possible values of $$\frac{f(x)}{g(x)}$$ ?
correct answer:- 4
Question 65
The figure below shows the graph of a function f(x). How many solutions does the equation f(f(x)) = 15 have?
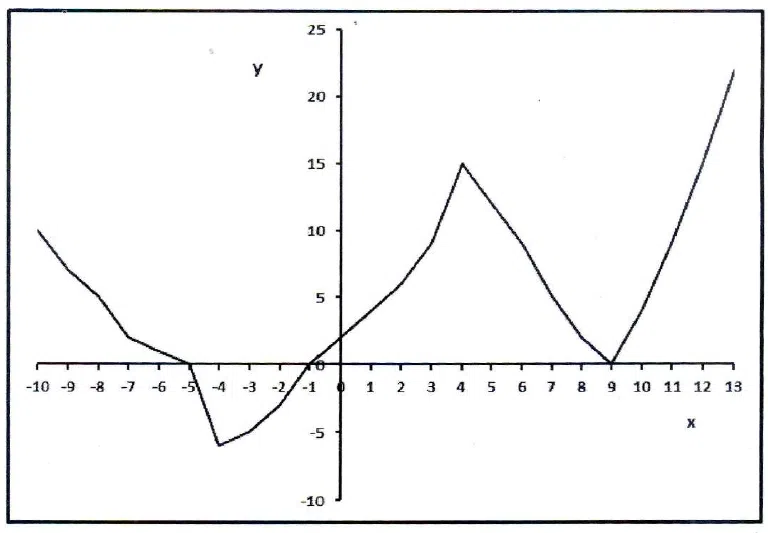
correct answer:- 3
Question 66
In a list of 7 integers, one integer, denoted as x is unknown. The other six integers are 20, 4, 10, 4,8, and 4. If the mean, median, and mode of these seven integers are arranged in increasing order, they form an arithmetic progression. The sum of all possible values of x is
correct answer:- 5
Let $$A_{1},A_{2},.....A_{n}$$ be then points on the straight - line y = px + q. The coordinates of $$A_{k}is(X_{k},Y_{k})$$, where k = 1, 2, ...n such that $$X_{1},X_{2}....X_{n}$$ are in arithmetic progression. The coordinates of $$A_{2}$$ is (2,–2) and $$A_{24}$$ is (68, 31).
Question 67
The number of point(s) satisfying the above mentioned characteristics and not in the first quadrant is/are
correct answer:- 3
Question 68
A shop sells bags in three sizes: small, medium and large. A large bag costs Rs.1000, a medium bag costs Rs.200, and a small bag costs Rs.50. Three buyers, Ashish, Banti and Chintu, independently buy some numbers of these types of bags. The respective amounts spent by Ashish, Banti and Chintu are equal. Put together, the shop sells 1 large bag, 15 small bags and some medium bags to these three buyers. What is the minimum number of medium bags that the shop sells to them?
correct answer:- 5
Question 69
The roots of the polynomial $$P(x) = 2x^3 - 11x^2 + 17x - 6$$ are the radii of three concentric circles.
The ratio of their area, when arranged from the largest to the smallest, is:
correct answer:- 4
Question 70
If $$x$$ and $$y$$ are real numbers, the least possible value of the expression $$4(x - 2)^{2} + 4(y - 3)^{2} - 2(x - 3)^{2}$$ is :
correct answer:- 2
Question 71
a, b, c are integers, |a| ≠ |b| ≠|c| and -10 ≤ a, b, c ≤ 10. What will be the maximum possible value of [abc - (a + b + c)]?
correct answer:- 3
Question 72
When opening his fruit shop for the day a shopkeeper found that his stock of apples could be perfectly arranged in a complete triangular array: that is, every row with one apple more than the row immediately above, going all the way up ending with a single apple at the top.
During any sales transaction, apples are always picked from the uppermost row, and going below only when that row is exhausted.
When one customer walked in the middle of the day she found an incomplete array in display having 126 apples totally. How many rows of apples (complete and incomplete) were seen by this customer? (Assume that the initial stock did not exceed 150 apples.)
correct answer:- 4
Question 73
Let x and y be two positive integers and p be a prime number. If x (x - p) - y (y + p) = 7p, what will be the minimum value of x - y?
correct answer:- 5
Question 74
The sum of the cubes of two numbers is 128, while the sum of the reciprocals of their cubes is 2.
What is the product of the squares of the numbers?
correct answer:- 3
Question 75
Consider the expression $$\frac{(a^2+a+1)(b^2+b+1)(c^2+c+1)(d^2+d+1)(e^2+e+1)}{abcde}$$, where a,b,c,d and e are positive numbers. The minimum value of the expression is
correct answer:- 5
Question 76
For a positive integer x, define f(x) such that f(x + a) = f(a × x), where a is an integer and f(1) = 4. If the value of f(1003) = k, then the value of ‘k’ will be:
correct answer:- 5
Question 77
A marble is dropped from a height of 3 metres onto the ground. After hitting the ground, it bounces and reaches 80% of the height from which it was dropped. This repeats multiple times. Each time it bounces, the marble reaches 80% of the height previously reached. Eventually, the marble comes to rest on the ground.
What is the maximum distance that the marble travels from the time it was dropped until it comes to rest?
correct answer:- 2
Question 78
The mean of six positive integers is 15. The median is 18, and the only mode of the integers is less than 18. The maximum possible value of the largest of the six integers is
correct answer:- 4
Question 79
If $$x=(9+4\sqrt{5})^{48} = [x] +f$$, where [x] is defined as integral part of x and f is a fraction, then x (1 - f) equals
correct answer:- 1
Question 80
Consider the four variables A, B, C and D and a function Z of these variables, $$Z = 15A^2 - 3B^4 + C + 0.5D$$ It is given that A, B, C and D must be non-negative integers and thatall of the following relationships must hold:
i) $$2A + B \leq 2$$
ii) $$4A + 2B + C \leq 12$$
iii) $$3A + 4B + D \leq 15$$
If Z needs to be maximised, then what value must D take?
correct answer:- 2
Question 81
a, b, c, d and e are integers such that 1 ≤ a < b < c < d < e. If a, b, c, d and e are geometric
progression
and lcm (m , n) is the least common multiple of m and n, then the maximum value of $$\frac{1}{lcm(a,b)}+\frac{1}{lcm(b,c)}+\frac{1}{lcm(c,d)}+\frac{1}{lcm(d,e)}$$ is
correct answer:- 2
Question 82
Find z, if it is known that:
a: $$-y^2 + x^2 = 20$$
b: $$y^3 - 2x^2 - 4z \geq -12$$ and
c: x, y and z are all positive integers
correct answer:- 5
Question 83
Consider the system of two linear equations as follows: $$3x + 21y + p = 0$$; and $$qx + ry - 7 = 0$$, where p, q, and r are real numbers.
Which of the following statements DEFINITELY CONTRADICTS the fact that the lines represented by the two equations are coinciding?
correct answer:- 3
Question 84
What is the sum of the following series?
-64, -66, -68,............., -100
correct answer:- 2
Question 85
A chocolate dealer has to send chocolates of three brands to a shopkeeper. All the brands are packed in boxes of same size. The number of boxes to be sent is 96 of brand A, 240 of brand B and 336 of brand C. These boxes are to be packed in cartons of same size containing equal number of boxes. Each carton should contain boxes of same brand of chocolates. What could be the minimum number of cartons that the dealer has to send?
correct answer:- 2
Question 86
If both the sequences x, a1, a2, y and x, b1, b2, z are in A.P. and it is given that $$y > x$$ and $$z < x$$, then which of the following values can $$\left\{\frac{(a1-a2)}{(b1-b2)}\right\}$$ possibly take?
correct answer:- 3
Question 87
Consider the function f(x) = (x + 4)(x + 6)(x + 8) ⋯ (x + 98). The number of integers x for which f(x) < 0 is:
correct answer:- 3
Question 88
The operation (
x
)
is defined by
(i) (1) = 2
(ii)(x + y) = (x).(y)
for all positive integers x and y.
If $$\sum_{x=1}^n(x)$$ = 1022 then n =
correct answer:- 2
Question 89
If $$2 \leq |x - 1| \times |y + 3| \leq 5$$ and both $$x$$ and $$y$$ are negative integers, find the number of possible combinations of $$x$$ and $$y$$.
correct answer:- 5
Question 90
Consider the set of numbers {1, 3, $$3^{2}$$, $$3^{3}$$,…...,$$3^{100}$$}. The ratio of the last number and the sum of the remaining numbers is closest to:
correct answer:- 2
Question 91
The sum of series, (-100) + (-95) + (-90) + …………+ 110 + 115 + 120, is:
correct answer:- 4
Question 92
p, q and r are three non-negative integers such that p + q + r = 10. The maximum value of pq + qr + pr + pqr is
correct answer:- 3
Question 93
The sum of the possible values of X in the equation |X + 7| + |X - 8| = 16 is:
correct answer:- 2
Question 94
The Guava club has won 40% of their football matches in the Apple Cup that they have played so far. If they play another n matches and win all of them, their winning percentage will improve to 50. Further, if they play 15 more matches and win all of them, their winning percentage will improve from 50 to 60. How many matches has the Guava club played in the Apple Cup so far? In the Apple Cup matches, there are only two possible outcomes, win or loss; draw is not possible.
correct answer:- 1
Question 95
Find the equation of the graph shown below.
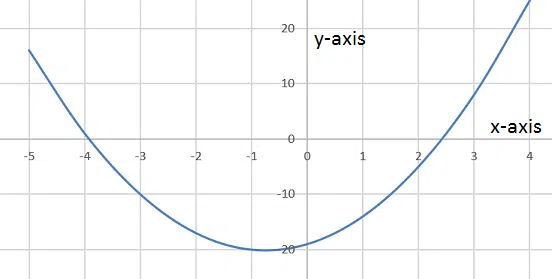
correct answer:- 4
Question 96
Three truck drivers, Amar, Akbar and Anthony stop at a road side eating joint. Amar orders 10
rotis, 4 plates of tadka, and a cup of tea. Akbar orders 7 rotis, 3 plates of tadka, and a cup of tea. Amar pays 80 for the meal and Akbar pays 60. Meanwhile, Anthony orders 5 rotis, 5 plates of tadka and 5 cups of tea. How much (in ) will Anthony pay?
correct answer:- 4
Question 97
f is a function for which f(1)= 1 and f(x) = 2x + f(x - 1) for each natural number x$$\geq$$2. Find f(31)
correct answer:- 4
Question 98
Rahul has just made a $$3 \times 3$$ magic square, in which, the sum of the cells along any row, column or diagonal, is the same number N. The entries in the cells are given as expressions in x, y, and Z. Find N?

correct answer:- 2
Question 99
Given that a and b are integers and that $$5x+2\sqrt{7}$$ is a root of the polynomial $$x^2 - ax + b + 2\sqrt{7}$$ in $$x$$, what is the value of b?
correct answer:- 1
Let $$A_{1},A_{2},.....A_{n}$$ be then points on the straight - line y = px + q. The coordinates of $$A_{k}is(X_{k},Y_{k})$$, where k = 1, 2, ...n such that $$X_{1},X_{2}....X_{n}$$ are in arithmetic progression. The coordinates of $$A_{2}$$ is (2,–2) and $$A_{24}$$ is (68, 31).
Question 100
The y - ordinates of $$A_8$$ is
correct answer:- 3
Question 101
A polynomial y=$$ax^{3} + bx^{2 }+ cx + d$$ intersects x-axis at 1 and -1, and y-axis at 2. The value of b is:
correct answer:- 1
Question 102
a, b, c are integers, |a| ≠ |b| ≠|c| and -10 ≤ a, b, c ≤ 10. What will be the maximum possible value of [abc - (a + b + c)]?
correct answer:- 3
Read the following scenario and answer the TWO questions that follow.
Aman has come to the market with Rs. 100. If he buys 5 kilograms of cabbage and 4 kilograms of potato, he will have Rs. 20 left; or else, if he buys 4 kilograms of cabbage and 5 kilograms of onion, he will have Rs. 7 left. The per kilogram prices of cabbage, onion and potato are positive integers (in rupees), and any type of these vegetables can only be purchased in positive integer kilogram, or none at all.
Question 103
Aman decides to buy only onion, in whatever maximum quantity possible (in positive integer kilogram), with the money he has come to the market with. How much money will he be left with after the purchase?
correct answer:- 5
Question 104
Consider $$a_{n+1} =\frac{1}{1+\frac{1}{a_{n}}}$$ for $$n = 1,2, ....., 2008, 2009$$ where $$a_{1} = 1$$. Find the value of $$a_{1}a_{2} + a_{2}a_{3} + a_{3}a_{4} + ... + a_{2008}a_{2009}$$.
correct answer:- 3
Question 105
Shireen draws a circle in her courtyard. She then measures the circle’s circumference and its diameter with her measuring tape and records them as two integers, A and B respectively. She finds that A and B are co-primes, that is, their greatest common divisor is 1. She also finds their ratio, A:B, to be: 3.141614161416… (repeating endlessly).
What is A - B ?
correct answer:- 2
Question 106
Some members of a social service organization in Kolkata decide to prepare 2400 laddoos to gift to children in various orphanages and slums in the city, during Durga puja. The plan is that each of them makes the same number of laddoos. However, on the laddoo-making day, ten members are absent, thus each remaining member makes 12 laddoos more than earlier decided.
How many members actually make the laddoos?
correct answer:- 5
Question 107
If $$x^2 + x + 1 = 0$$, then $$x^{2018} + x^{2019}$$ equals which of the following:
correct answer:- 3
Question 108
Consider the quadratic function $$f(x) = ax^2 + bx + a$$ having two irrational roots, with a and b being two positive integers, such that $$a, b \leq 9$$.
If all such permissible pairs (a, b) are equally likely, what is the probability that a + b is greater than 9?
correct answer:- 4
Question 109
Consider a function $$f(x) = x^4 + x^3 + x^2 + x + 1$$, where x is a positive integer greater than 1. What will be the remainder if $$f(x^5)$$ is divided by f(x)?
correct answer:- 1
Question 110
Determine the value(s) of “a” for which the point $$(a, a^{2})$$ lies inside the triangle formed by the lines: 2x+ 3y= 1, x+ 2y=3 and 5x-6y= 1
correct answer:- 3
Question 111
If f(x) = ax + b, a and b are positive real numbers and if f(f(x)) = 9x + 8, then the value of a + b is:
correct answer:- 3
Question 112
Let $$a_{n} = 1 1 1 1 1 1 1..... 1$$, where 1 occurs n number of times. Then,
i. $$a_{741}$$ is not a prime.
ii. $$a_{534}$$ is not a prime.
iii. $$a_{123}$$ is not a prime.
iv. $$a_{77}$$ is not a prime.
correct answer:- 4
Question 113
Two different quadratic equations have a common root. Let the three unique roots of the two equations be A, B and C - all of them are positive integers. If (A + B + C) = 41 and the product of the roots of one of the equations is 35, which of the following options is definitely correct?
correct answer:- 3
Question 114
Consider the real-valued function $$f(x)=\frac{\log{(3x-7)}}{\sqrt{2x^{2}-7x+6}}$$ Find the domain of f(x).
correct answer:- 1
Question 115
The cost of running a movie theatre is Rs. 10,000 per day, plus additional Rs. 5000 per show. The theatre has 200 seats. A new movie released on Friday. There were three shows, where the ticket price was Rs. 250 each for the first two shows and Rs. 200 for the late-night show.
For all shows together, total occupancy was 80%. What was the maximum amount of profit possible?
correct answer:- 4
Question 116
Consider the set of numbers {1, 3, $$3^{2}$$, $$3^{3}$$,…...,$$3^{100}$$}. The ratio of the last number and the sum of the remaining numbers is closest to:
correct answer:- 2








.webp)











































