Most Important XAT Algebra Question
Algebra is an important part of the XAT exam, and doing well in this section can help increase your overall score. Algebra questions in XAT test your understanding of topics like equations, inequalities, functions, and number relationships. These questions also check your logical thinking and problem-solving skills. We have selected the most important Algebra questions covering key topics such as linear equations, quadratic equations, functions, and progressions that are commonly asked in XAT.
This blog is a complete guide to Algebra for XAT, with questions from easy to difficult levels. Each topic is explained in a simple and easy-to-understand way. Whether you are practicing equations, learning algebraic identities, or understanding functions, regular practice will help you improve speed and accuracy and feel more confident for the XAT exam.
Download XAT Algebra Questions PDF
To make your preparation easier, we have created a downloadable PDF with the most important Algebra questions for XAT. The PDF covers key topics like linear equations, quadratic equations, functions, and sequences. It is useful for daily practice and quick revision, so you can study anytime and anywhere. Download the XAT Algebra Questions PDF now and strengthen your Algebra preparation.
List of Important Algebra Questions for XAT 2026
Question 1
Find z, if it is known that:
a: $$-y^2 + x^2 = 20$$
b: $$y^3 - 2x^2 - 4z \geq -12$$ and
c: x, y and z are all positive integers
correct answer:- 5
Question 2
Consider the real-valued function $$f(x)=\frac{\log{(3x-7)}}{\sqrt{2x^{2}-7x+6}}$$ Find the domain of f(x).
correct answer:- 1
Question 3
A chocolate dealer has to send chocolates of three brands to a shopkeeper. All the brands are packed in boxes of same size. The number of boxes to be sent is 96 of brand A, 240 of brand B and 336 of brand C. These boxes are to be packed in cartons of same size containing equal number of boxes. Each carton should contain boxes of same brand of chocolates. What could be the minimum number of cartons that the dealer has to send?
correct answer:- 2
Question 4
The Guava club has won 40% of their football matches in the Apple Cup that they have played so far. If they play another n matches and win all of them, their winning percentage will improve to 50. Further, if they play 15 more matches and win all of them, their winning percentage will improve from 50 to 60. How many matches has the Guava club played in the Apple Cup so far? In the Apple Cup matches, there are only two possible outcomes, win or loss; draw is not possible.
correct answer:- 1
Question 5
A polynomial y=$$ax^{3} + bx^{2 }+ cx + d$$ intersects x-axis at 1 and -1, and y-axis at 2. The value of b is:
correct answer:- 1
Question 6
Consider the system of two linear equations as follows: $$3x + 21y + p = 0$$; and $$qx + ry - 7 = 0$$, where p, q, and r are real numbers.
Which of the following statements DEFINITELY CONTRADICTS the fact that the lines represented by the two equations are coinciding?
correct answer:- 3
Question 7
p, q and r are three non-negative integers such that p + q + r = 10. The maximum value of pq + qr + pr + pqr is
correct answer:- 3
Question 8
For a positive integer x, define f(x) such that f(x + a) = f(a × x), where a is an integer and f(1) = 4. If the value of f(1003) = k, then the value of ‘k’ will be:
correct answer:- 5
Question 9
Consider the expression $$\frac{(a^2+a+1)(b^2+b+1)(c^2+c+1)(d^2+d+1)(e^2+e+1)}{abcde}$$, where a,b,c,d and e are positive numbers. The minimum value of the expression is
correct answer:- 5
Question 10
Let x and y be two positive integers and p be a prime number. If x (x - p) - y (y + p) = 7p, what will be the minimum value of x - y?
correct answer:- 5
Question 11
The sum of the possible values of X in the equation |X + 7| + |X - 8| = 16 is:
correct answer:- 2
Question 12
Let $$f(x) = \frac{x^2 + 1}{x^2 - 1}$$ if $$x \neq 1, -1,$$ and 1 if x = 1, -1. Let $$g(x) = \frac{x + 1}{x - 1}$$ if $$x \neq 1,$$ and 3 if x = 1.
What is the minimum possible values of $$\frac{f(x)}{g(x)}$$ ?
correct answer:- 4
Question 13
If $$x^2 + x + 1 = 0$$, then $$x^{2018} + x^{2019}$$ equals which of the following:
correct answer:- 3
Question 14
If f(x) = ax + b, a and b are positive real numbers and if f(f(x)) = 9x + 8, then the value of a + b is:
correct answer:- 3
Question 15
The mean of six positive integers is 15. The median is 18, and the only mode of the integers is less than 18. The maximum possible value of the largest of the six integers is
correct answer:- 4
Let $$A_{1},A_{2},.....A_{n}$$ be then points on the straight - line y = px + q. The coordinates of $$A_{k}is(X_{k},Y_{k})$$, where k = 1, 2, ...n such that $$X_{1},X_{2}....X_{n}$$ are in arithmetic progression. The coordinates of $$A_{2}$$ is (2,–2) and $$A_{24}$$ is (68, 31).
Question 16
The number of point(s) satisfying the above mentioned characteristics and not in the first quadrant is/are
correct answer:- 3
Question 17
Given $$A = |x + 3| + | x - 2 | - | 2x -8|$$. The maximum value of $$|A|$$ is:
correct answer:- 2
Question 18
The operation (
x
)
is defined by
(i) (1) = 2
(ii)(x + y) = (x).(y)
for all positive integers x and y.
If $$\sum_{x=1}^n(x)$$ = 1022 then n =
correct answer:- 2
Question 19
If $$x=(9+4\sqrt{5})^{48} = [x] +f$$, where [x] is defined as integral part of x and f is a fraction, then x (1 - f) equals
correct answer:- 1
Question 20
The roots of the polynomial $$P(x) = 2x^3 - 11x^2 + 17x - 6$$ are the radii of three concentric circles.
The ratio of their area, when arranged from the largest to the smallest, is:
correct answer:- 4
Question 21
Find the equation of the graph shown below.
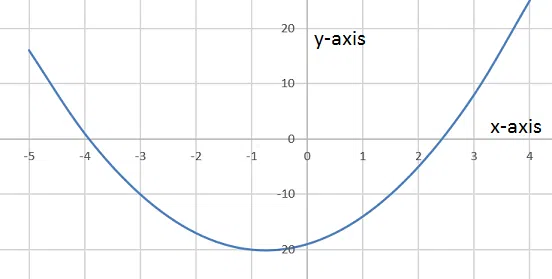
correct answer:- 4
Question 22
a, b, c are integers, |a| ≠ |b| ≠|c| and -10 ≤ a, b, c ≤ 10. What will be the maximum possible value of [abc - (a + b + c)]?
correct answer:- 3
Question 23
If $$2 \leq |x - 1| \times |y + 3| \leq 5$$ and both $$x$$ and $$y$$ are negative integers, find the number of possible combinations of $$x$$ and $$y$$.
correct answer:- 5
Question 24
The sum of the cubes of two numbers is 128, while the sum of the reciprocals of their cubes is 2.
What is the product of the squares of the numbers?
correct answer:- 3
Question 25
Determine the value(s) of “a” for which the point $$(a, a^{2})$$ lies inside the triangle formed by the lines: 2x+ 3y= 1, x+ 2y=3 and 5x-6y= 1
correct answer:- 3
Question 26
Given that a and b are integers and that $$5x+2\sqrt{7}$$ is a root of the polynomial $$x^2 - ax + b + 2\sqrt{7}$$ in $$x$$, what is the value of b?
correct answer:- 1
Question 27
If $$\log_4m + \log_4n = \log_2(m + n)$$ where m and n are positive real numbers, then which of the following must be true?
correct answer:- 5
Question 28
Consider the equation $$\log_5(x - 2) = 2 \log_{25}(2x - 4)$$, where x is a real number.
For how many different values of x does the given equation hold?
correct answer:- 1
Question 29
If $$f(x^2 - 1) = x^4 - 7x^2 + k_1$$ and $$f(x^3 - 2) = x^6 - 9x^3 +k_2$$ then the value of $$(k_2 - k_1)$$ is
correct answer:- 3
Question 30
For how many distinct real values of $$x$$ does the equation below hold true? (Consider $$a$$ > 0.)
$$\dfrac{x^2 \log_a(16)}{\log_a(32)} - \dfrac{\log_a(64)}{\log_a(32)} - x = 0 $$
correct answer:- 5
Question 31
If $$x$$ and $$y$$ are real numbers, the least possible value of the expression $$4(x - 2)^{2} + 4(y - 3)^{2} - 2(x - 3)^{2}$$ is :
correct answer:- 2
Question 32
For a positive integer x, define f(x) such that f(x + a) = f(a × x), where a is an integer and f(1) = 4. If the value of f(1003) = k, then the value of ‘k’ will be:
correct answer:- 5
Question 33
The figure below shows the graph of a function f(x). How many solutions does the equation f(f(x)) = 15 have?
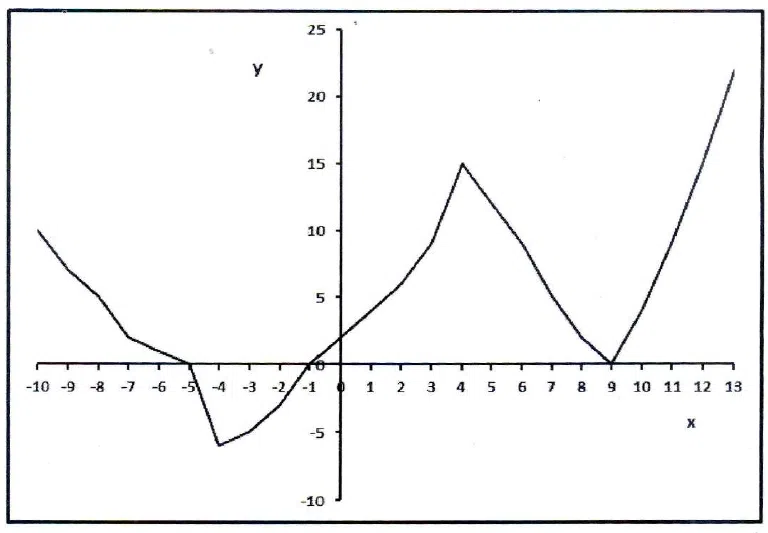
correct answer:- 3
Question 34
The domain of the function $$f(x) =log_{7}({ log_{3}(log_{5}(20x-x^{2}-91 )))}$$ is:
correct answer:- 2
Question 35
Consider the function f(x) = (x + 4)(x + 6)(x + 8) ⋯ (x + 98). The number of integers x for which f(x) < 0 is:
correct answer:- 3
Let $$A_{1},A_{2},.....A_{n}$$ be then points on the straight - line y = px + q. The coordinates of $$A_{k}is(X_{k},Y_{k})$$, where k = 1, 2, ...n such that $$X_{1},X_{2}....X_{n}$$ are in arithmetic progression. The coordinates of $$A_{2}$$ is (2,–2) and $$A_{24}$$ is (68, 31).
Question 36
The y - ordinates of $$A_8$$ is
correct answer:- 3
Question 37
The value of the expression: $$\sum_{i=2}^{100}\frac{1}{log_{i}100!}$$ is:
correct answer:- 3
Question 38
Consider the four variables A, B, C and D and a function Z of these variables, $$Z = 15A^2 - 3B^4 + C + 0.5D$$ It is given that A, B, C and D must be non-negative integers and thatall of the following relationships must hold:
i) $$2A + B \leq 2$$
ii) $$4A + 2B + C \leq 12$$
iii) $$3A + 4B + D \leq 15$$
If Z needs to be maximised, then what value must D take?
correct answer:- 2
Question 39
$$\frac{log (97-56\sqrt{3})}{log \sqrt{7+4\sqrt{3}}}$$ equals which of the following?
correct answer:- 3
Question 40
Two different quadratic equations have a common root. Let the three unique roots of the two equations be A, B and C - all of them are positive integers. If (A + B + C) = 41 and the product of the roots of one of the equations is 35, which of the following options is definitely correct?
correct answer:- 3
Question 41
Rahul has just made a $$3 \times 3$$ magic square, in which, the sum of the cells along any row, column or diagonal, is the same number N. The entries in the cells are given as expressions in x, y, and Z. Find N?

correct answer:- 2
Question 42
Consider the quadratic function $$f(x) = ax^2 + bx + a$$ having two irrational roots, with a and b being two positive integers, such that $$a, b \leq 9$$.
If all such permissible pairs (a, b) are equally likely, what is the probability that a + b is greater than 9?
correct answer:- 4
Read the following scenario and answer the TWO questions that follow.
Aman has come to the market with Rs. 100. If he buys 5 kilograms of cabbage and 4 kilograms of potato, he will have Rs. 20 left; or else, if he buys 4 kilograms of cabbage and 5 kilograms of onion, he will have Rs. 7 left. The per kilogram prices of cabbage, onion and potato are positive integers (in rupees), and any type of these vegetables can only be purchased in positive integer kilogram, or none at all.
Question 43
Aman decides to buy only onion, in whatever maximum quantity possible (in positive integer kilogram), with the money he has come to the market with. How much money will he be left with after the purchase?
correct answer:- 5
Question 44
f is a function for which f(1)= 1 and f(x) = 2x + f(x - 1) for each natural number x$$\geq$$2. Find f(31)
correct answer:- 4
Let $$A_{1},A_{2},.....A_{n}$$ be then points on the straight - line y = px + q. The coordinates of $$A_{k}is(X_{k},Y_{k})$$, where k = 1, 2, ...n such that $$X_{1},X_{2}....X_{n}$$ are in arithmetic progression. The coordinates of $$A_{2}$$ is (2,–2) and $$A_{24}$$ is (68, 31).
Question 45
The number of point(s) satisfying the above mentioned characteristics and not in the first quadrant is/are
correct answer:- 3
Question 46
The Guava club has won 40% of their football matches in the Apple Cup that they have played so far. If they play another n matches and win all of them, their winning percentage will improve to 50. Further, if they play 15 more matches and win all of them, their winning percentage will improve from 50 to 60. How many matches has the Guava club played in the Apple Cup so far? In the Apple Cup matches, there are only two possible outcomes, win or loss; draw is not possible.
correct answer:- 1
Question 47
Find the equation of the graph shown below.
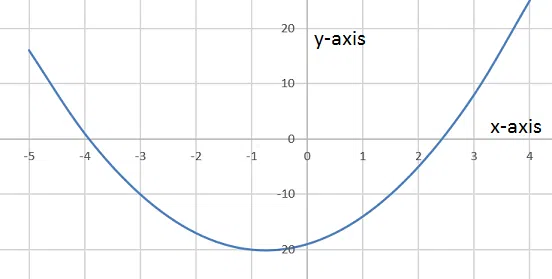
correct answer:- 4
 Group
Group







.webp)

























