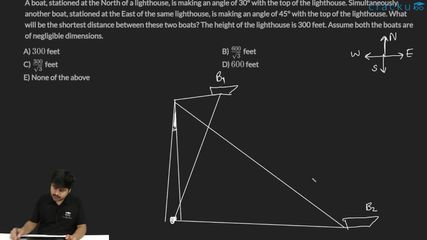
A boat, stationed at the North of a lighthouse, is making an angle of 30° with the top of the lighthouse. Simultaneously, another boat, stationed at the East of the same lighthouse, is making an angle of 45° with the top of the lighthouse. What will be the shortest distance between these two boats? The height of the lighthouse is 300 feet. Assume both the boats are of negligible dimensions.
Solution
One boat is stationed to the North of the light house and the other boat is stationed to the East of the light house.

The boat stationed to the East subtends an angle of 45 degrees and the boat stationed to the North subtends an angle of 30 degrees.
Now, distance between the boat stationed to the East and the light house,d1 = tan 45
$$300/d1 = 1$$
=> $$d1 = 300$$ feet
Distance between the boat stationed to the North and the light house,d2 = tan 30
$$300/d2 = 1/\sqrt{3}$$
=> $$d2=300\sqrt{3}$$
Shortest distance between the 2 boats = $$\sqrt{300^2+(300\sqrt{3})^2}$$
= $$300*\sqrt{4}$$
= $$600$$ feet.
Therefore, option C is the right answer.
Video Solution
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
