ABC is a triangle with integer-valued sides AB = 1, BC >1, and CA >1. If D is the mid-point of AB, then, which of the following options is the closest to the maximum possible value of the angle ACD (in degrees)?
Solution
We will try to maximize the value of the angle ACD:
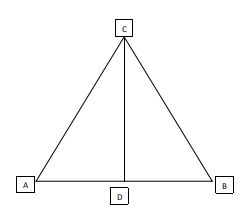
For a fixed triangle ABC, the angle ACD can be maximized when we take the median CD to be perpendicular to AB and the value of AC is as small as possible, so that the sine of angle ACD, and hence, the angle ACD itself if maximized, as the value of AD is fixed at half of AB at 0.5.
Now, the least possible value of AC is 2. The triangle will be of sides (1,2,2).
Value of sin(ACD)=$$\frac{0.5}{2}=0.25$$
$$\angle\ ACD=\sin^{-1}\left(0,25\right)=14.78\approx\ 15.$$
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
