Instructions

For the following questions answer them individually

Question 1

If $$\log_4m + \log_4n = \log_2(m + n)$$ where m and n are positive real numbers, then which of the following must be true?

Video Solution

Solution

$$\log_4mn=\log_2(m+n)$$

$$\sqrt{\ mn}=(m+n)$$

Squarring on both sides

$$m^2+n^2+mn\ =\ 0$$

Since m, n are positive real numbers, no value of m and n satisfy the above equations.

Question 2

Mr. Jose buys some eggs. After bringing the eggs home, he finds two to be rotten and throws them away. Of the remaining eggs, he puts five-ninth in his fridge, and brings the rest to his mother’s house. She cooks two eggs and puts the rest in her fridge. If her fridge cannot hold more than five eggs, what is the maximum possible number of eggs bought by Mr. Jose?

Video Solution

Solution

Let the number of eggs bought = 9x+2

number of eggs left after throwing away 2 = 9x

number of eggs kept in fridge = 5x

number of eggs brought to his mothers' house = 4x

number of eggs left after cooking 2 which are kept in fridge = 4x-2

Given, 4x-2 <=5

=> x$$\le\frac{7}{4}$$

Hence the max value of x is 1

Max number of eggs bought = 11

Question 3

Mohan has some money (₹M) that he divides in the ratio of 1:2. He then deposits the smaller amount in a savings scheme that offers a certain rate of interest, and the larger amount in another savings scheme that offers half of that rate of interest. Both interests compound yearly. At the end of two years, the total interest earned from the two savings schemes is ₹830. It is known that one of the interest rates is 10% and that Mohan deposited more than ₹1000 in each saving scheme at the start. What is the value of M?

Video Solution

Solution

Let the total amount be 3x

Case 1:

Smaller amount = x, rate of interest = 10

Larger amount = 2x, rate of interest = 5

Total amount received at the end of two years( smaller amount) = $$x\left(1+\frac{10}{100}\right)^2\ =\ 1.21x$$. CI = 0.21x

Total amount received at the end of two years( larger amount) = $$2x\left(1+\frac{5}{100}\right)^2\ =\ 2.205x$$ CI = 0.205x

Given, 0.21x + 0.205x = 830

=> x = 2000

2x= 4000

Case 2:

Smaller amount = x, rate of interest = 20

Larger amount = 2x, rate of interest = 10

Total amount received at the end of two years( smaller amount) = $$x\left(1+\frac{20}{100}\right)^2\ =\ 1.44x$$. CI = 0.44x

Total amount received at the end of two years( larger amount) = $$2x\left(1+\frac{10}{100}\right)^2\ =\ 2.42x$$ CI = 0.42x

Given, 0.44x+0.42x = 830

=> x = 965.11 which is not valid since it should be greater than 1000

Question 4

A small store has five units of a new phone model in stock: two white, two black, and one red. Three customers arrive at the shop to buy a unit each. Each one has a pre- determined choice of the colour and will not buy a unit of any other colour. All the three customers are equally likely to have chosen any of the three colours. What is the probability that the store will be able to satisfy all the three customers?

Video Solution

Solution

Number of white phones = 2

Number of black phones = 2

Number of red phones = 1

customer 1 will have 3 choices

customer 2 will have 3 choices

customer 3 will have 3 choices

Hence total choices = 3 x 3 x 3 = 27

The cases not possible = BBB, RRR,WWW, RRB,RBR,BRR, RRW,RWR, WRR

Possible cases = 18

Probability = 18/27 = 2/3

Question 5

At any point of time, let x be the smaller of the two angles made by the hour hand with the minute hand on an analogue clock (in degrees). During the time interval from 2:30 p.m. to 3:00 p.m., what is the minimum possible value of x?

Video Solution

Solution

The difference between the hour and minute hand of a clock is given by $$\left|30H-5.5m\right|$$. Here H is the current hour and m represents the number of completed minutes in the current hour.

In the given time frame of 2: 30 to 3: 00 pm.

At 2 : 30 pm the angle = $$\left|30\cdot2-5.5\cdot30\right|\ =\ 105\ \deg rees$$

At 3: 00 pm the angle = $$\left|30\cdot3-5.5\cdot0\right|\ =\ 90\ \deg rees$$

The function of $$\left|30\cdot H-5.5\cdot m\right|\ =\ $$ constantly increases as the value of m increases from 31, 32................ 59.

Because of the modulus function, the net value of the function remains positive

Between 2: 30 to 2: 59 the angle is constantly increasing. The minimum value is 2: 30 which is equal to 105 degrees which is greater than the 90 degrees when the time is 3: 00.

Hence 90 degrees is the minimum angle.

Question 6

One third of the buses from City A to City B stop at City C, while the rest go non-stop to City B. One third of the passengers, in the buses stopping at City C, continue to City B, while the rest alight at City C. All the buses have equal capacity and always start full from City A. What proportion of the passengers going to City B from City A travel by a bus stopping at City C?

Video Solution

Solution

Let us assume there are 9 buses.

3 of them stop at C and 6 go non-stop

Given, One-third of the passengers, in the buses stopping at City C, continue to City B, while the rest alight at City C

=> Since all buses have equal capacity. we can say 2 will elite at C and 1 will proceed to B.

Hence required proportion = 1/7

Question 7

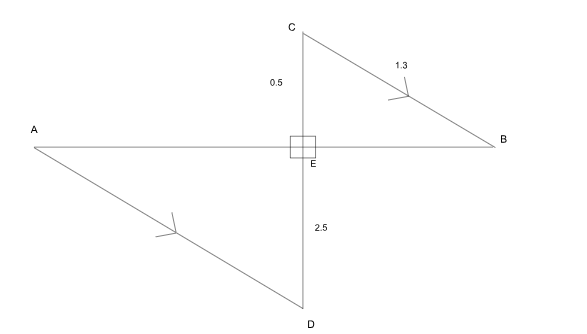
Rajesh, a courier delivery agent, starts at point A and makes a delivery each at points B, C and D, in that order. He travels in a straight line between any two consecutive points. The following are known: (i) AB and CD intersect at a right angle at E, and (ii) BC, CE and ED are respectively 1.3 km, 0.5 km and 2.5 km long. If AD is parallel to BC, then what is the total distance (in km) that Rajesh covers in travelling from A to D?

Video Solution

Solution

Given, CE=0.5, BC = 1.3 and ED=2.5

Triangle CEB is a right-angled triangle => EB = 1.2

Triangles ECB is similar to triangle EDA

EB/EC = AE/ED => AE = 6

Hence total distance travelled = AB + BC + CD = 7.2 + 1.3 + 3.5 = 11.5km

Question 8

Let $$f(x) = \frac{x^2 + 1}{x^2 - 1}$$ if $$x \neq 1, -1,$$ and 1 if x = 1, -1. Let $$g(x) = \frac{x + 1}{x - 1}$$ if $$x \neq 1,$$ and 3 if x = 1.
What is the minimum possible values of $$\frac{f(x)}{g(x)}$$ ?

Video Solution

Solution

$$\frac{f\left(x\right)}{g\left(x\right)}=\frac{\left(x^2+1\right)}{x^2-1}\cdot\frac{\left(x-1\right)}{x+1}=\frac{\left(x^2+1\right)}{\left(x+1\right)^2}$$

This function is definitely greater than 0

$$let\ y=\frac{\left(x^2+1\right)}{\left(x+1\right)^2}$$

=> $$x^2\left(y-1\right)+2yx+\left(y-1\right)=0$$ which is quadratic in x

Disctiminant should be greater than 0

$$4y^2-4\left(y-1\right)^2\ge0$$

=> y>=1/2

When x =1, f(x)/g(x) = 1/3

Hence either the value should be greater than 1/2 or should be equal to 1/3

Question 9

Swati can row a boat on still water at a speed of 5 km/hr. However, on a given river, it takes her 1 hour more to row the boat 12 km upstream than downstream. One day, Swati rows the boat on this river from X to Y, which is N km upstream from X. Then she rows back to X immediately. If she takes at least 2 hours to complete this round trip, what is the minimum possible value of N?

Video Solution

Solution

Let the speed of the stream be x

$$\frac{12}{5-x}=\frac{12}{5+x}+1$$

The value of x satisfying the above equation is 1

Now,

$$\frac{N}{5+1}+\frac{N}{5-1}\ge2$$

$$\frac{2N+3N}{12}\ge2$$

=> $$N\ge4.8$$

Question 10

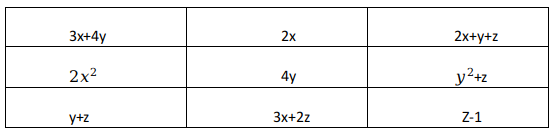
Rahul has just made a $$3 \times 3$$ magic square, in which, the sum of the cells along any row, column or diagonal, is the same number N. The entries in the cells are given as expressions in x, y, and Z. Find N?

Video Solution

Solution

Sum of 3rd row = sum of 2nd column

=> 2x+4y = y+2z-1

=> 2x+3y-2z= -1 ------- (A)

Sum of diagonals are also equal

=> 3x+4y+z-1 = y+z+2x+y+z

=> x+2y-z=1 -----(B)

Solving A and B we get y= 3

Putting it in A, we get x-z = -5 ----- (C)

Sum of 1st row = sum of 2nd column

5x+5y+z = 3x+4y+2z

=> 2x +y - z =0

Since y=3, 2x-z = -3 ------ (D)

Solving C and D we get x=2 and z=7

Hence N = 36

CAT Content

XAT 2021 Question Paper

If $$\log_4m + \log_4n = \log_2(m + n)$$ where m and n are positive real numbers, then which of the following must be true?

At any point of time, let x be the smaller of the two angles made by the hour hand with the minute hand on an analogue clock (in degrees). During the time interval from 2:30 p.m. to 3:00 p.m., what is the minimum possible value of x?

Let $$f(x) = \frac{x^2 + 1}{x^2 - 1}$$ if $$x \neq 1, -1,$$ and 1 if x = 1, -1. Let $$g(x) = \frac{x + 1}{x - 1}$$ if $$x \neq 1,$$ and 3 if x = 1.
What is the minimum possible values of $$\frac{f(x)}{g(x)}$$ ?

Rahul has just made a $$3 \times 3$$ magic square, in which, the sum of the cells along any row, column or diagonal, is the same number N. The entries in the cells are given as expressions in x, y, and Z. Find N?

Related Formulas With Tests

XAT Quant Questions | XAT Quantitative Ability

XAT DILR Questions | LRDI Questions For XAT

XAT Verbal Ability Questions | VARC Questions For XAT

Also Read

CAT Content