Hey Devanshi, 
Suppose that there are 9 people who are starting from city A. 
Now since all the buses have equal number of people, we can say that 
9/3 = 3 will go to city C and 9-3 = 6 will go directly to city B 
One-third of people at city C continue to city B, hence we can say that 3/3 = 1 will go to city B from city C. 
Total number of people in city B = 1+6 = 7 
Total number of people arriving in city B from C = 1 
Proportion of the passengers going to City B from City A travel by a bus stopping at City C = 1/7

Hi Shubham,
Now consider the case that there are 9 buses in total.
Of which 2/3rd of them directly reach the city B. Hence 6 buses reach B directly.
Of the remaining 3 buses which are actually stopping at city C, only 1/3 from each of the three buses stopping are reaching C.
Since there are three buses in total an equivalent of 3*(1/3) = 1 bus reaches city B.
Similarly, an equivalent of 3*(2/3) = 2 buses remain in city C.
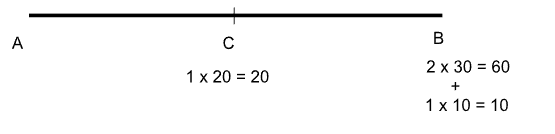
Hence now as per the question asked :
What proportion of the passengers going to City B from City A travel by bus stopping at City C?
Of the total of passengers in 9 buses. Only passengers equivalent to 7 buses reach city B. Other populations stay remained in the city B.
Of these people equivalent of 1 bus reaches city B.
Hence 1/7