XAT Temporary XAT Quant Questions
XAT 2025 Temporary XAT Quant questions
Question 1
There are 25 rooms in a hotel. Each room can accommodate at the most three people. For each room, the single occupancy charge is Rs. 2000 per day, the double occupancy charge is Rs. 3000 per day, and the triple occupancy charge is Rs. 3500 per day.
If there are 55 people staying in the hotel today, what is the maximum possible revenue from room occupancy charges today?
correct answer:-3
Question 2
An industrial robot manufacturing company is tasked to design humanoid robots to be used in warehouses where the robots need to pick items from a stack of shelves. The height of the topmost shelf from the ground is 7 feet. To operate, the robot has to move on a track, running parallel to the stack of shelves. The track is fixed 1 foot away from the base of the stack of shelves. Further, the robot cannot raise its arms by more than 60° from the horizontal plane.
If the robot’s arms are attached to its shoulder, what should be the minimum height of the robot from the ground to the shoulder for its arms to reach the topmost shelf?
correct answer:-3
Question 3
There are five dustbins along a circular path at different places. Ramesh takes multiple rounds of the path every morning, always at the same speed. He noticed that it took him a different number of steps to walk between any two consecutive dustbins. Ramesh also noticed that starting from any of the dustbins, it took a minimum 800 steps to reach every second dustbin. On the other hand, starting from any of the dustbins, it took a maximum 1260 steps to reach every third dustbin.
If Ramesh’s one step is 0.77 metre, and the width of the path is negligible, which the following can be the radius of the circular path?
correct answer:-4
Question 4
For how many distinct real values of $$x$$ does the equation below hold true? (Consider $$a$$ > 0.)
$$\dfrac{x^2 \log_a(16)}{\log_a(32)} - \dfrac{\log_a(64)}{\log_a(32)} - x = 0 $$
correct answer:-5
Question 5
A farmer has a quadrilateral parcel of land with a perimeter of 700 feet. Two opposite angles of that parcel of land are right angles, while the remaining two are not. The farmer wants to do organic farming on that parcel of land. The cost of organic farming is Rs. 400 per square foot.
Consider the following two additional pieces of information:
I. The length of one of the sides of that parcel of land is 110 feet.
II. The distance between the two corner points where the non-perpendicular sides of that parcel of land intersect is 255 feet.
To determine the amount of money the farmer needs to spend to do organic farming on the entire parcel of land, which of the above additional pieces of information is/are MINIMALLY SUFFICIENT?
correct answer:-3
Question 6
Consider the quadratic function $$f(x) = ax^2 + bx + a$$ having two irrational roots, with a and b being two positive integers, such that $$a, b \leq 9$$.
If all such permissible pairs (a, b) are equally likely, what is the probability that a + b is greater than 9?
correct answer:-4
Question 7
Eight employees of an organization have been rated on a scale of 1 to 50 for their performance. All ratings are integers. The overall average rating of the eight employees is 30. While the five employees with the highest ratings average 38, the five employees with the lowest ratings average 25.
Which of the following, about the ratings obtained by the eight employees, is DEFINITELY FALSE?
correct answer:-4
Question 8
Arun selected an integer $$x$$ between 2 and 40, both inclusive. He noticed that the greatest common divisor of the selected integer $$x$$ and any other integer between 2 and 40, both inclusive, is 1.
How many different choices for such an $$x$$ are possible?
correct answer:-1
Question 9
The market value of beams, made of a rare metal, has a unique property: the market value of any such beam is proportional to the square of its length. Due to an accident, one such beam got broken into two pieces having lengths in the ratio 4:9. Considering each broken piece as a separate beam, how much gain or loss, with respect to the market value of the original beam before the accident, is incurred?
correct answer:-2
Question 10
ABCD is a rectangle, where the coordinates of C and D are (- 2,0) and (2,0), respectively.
If the area of the rectangle is 24, which of the following is a possible equation representing the line $$\overleftrightarrow{AB}$$?
correct answer:-3
Question 11
Adu and Amu have bought two pieces of land on the Moon from an e-store. Both the pieces of land have the same perimeters, but Adu’s piece of land is in the shape of a square, while Amu’s piece of land is in the shape of a circle.
The ratio of the areas of Adu’s piece of land to Amu’s piece of land is:
correct answer:-4
Question 12
Ramesh bought a mobile from a local store. He paid 1/6 of the price via UPI and 1/3 of the price via cash. He agreed to pay the balance amount a year later. While paying back the balance amount, Ramesh paid 10% interest on the balance amount.
If the interest paid was Rs. 6000, what was the original price of the mobile?
correct answer:-1
Question 13
A straight line $$L_1$$ has the equation $$y = k(x - 1)$$, where k is some real number. The straight line $$L_1$$ intersects another straight line $$L_2$$ at the point (5, 8).
If $$L_2$$ has a slope of 1, which of the following is definitely FALSE?
correct answer:-1
Question 14
In a computer game, each move requires pressing a button. When the button is pressed for the first time, as a move, the computer randomly chooses a cell from a 4x4 grid of sixteen cells and puts an “X” mark on that cell. When the button is pressed subsequently, the computer randomly chooses a cell from the remaining unmarked cells and puts an “X” mark on that cell. This goes on till the end of the game. The game ends when either all the cells in any one row, or all the cells in any one column, are marked with “X”.
What is the maximum possible number of times a player has to press the button to finish the game?
correct answer:-4
Question 15
If a, b, and c are all positive integers, with 4a > b, then which of the following conditions is BOTH NECESSARY AND SUFFICIENT for the expression $$\sqrt[3]{(3)^a(21)^{(3a - b)}(49)^{(2b + c)}}$$ to be a positive integer?
correct answer:-5
Question 16
A soild trophy, consisting of two parts, has been designed in the following manner: the bottom part is a frustum of a cone with the bottom radius 30 cm, the top radius 20 cm, and height 40 cm, while the top part is a hemisphere with radius 20 cm. Moreover, the flat surface of the hemisphere is the same as the top surface of the frustum.
If the entire trophy is to be gold-plated at the cost of Rs. 40 per square cm, what would the cost for gold-plating be closest to?
correct answer:-3
Instruction for set 1:
Read the following scenario and answer the THREE questions that follow.
Comprehension:
In an 8-week course, a professor administered a test at the end of each week. Each of the eight tests was scored out of 4 marks, and a student could only receive a non-negative integer score.
Two students, Ravi and Sumana, took the eight tests.
In the first test, Ravi and Sumana scored the same marks. From the second to eighth tests, Ravi scored the exact same non-zero marks. Sumana scored the same marks as Ravi from the fifth test onwards. Ravi’s total marks in the first three tests was the same as Sumana’s total marks in the first two tests. Also, Sumana’s marks in the first test, total marks of the first two tests, and total marks of the eight tests are in a geometric progression.
Question 17
Which of the following CAN be true?
correct answer:-2
Instruction for set 1:
Read the following scenario and answer the THREE questions that follow.
Comprehension:
In an 8-week course, a professor administered a test at the end of each week. Each of the eight tests was scored out of 4 marks, and a student could only receive a non-negative integer score.
Two students, Ravi and Sumana, took the eight tests.
In the first test, Ravi and Sumana scored the same marks. From the second to eighth tests, Ravi scored the exact same non-zero marks. Sumana scored the same marks as Ravi from the fifth test onwards. Ravi’s total marks in the first three tests was the same as Sumana’s total marks in the first two tests. Also, Sumana’s marks in the first test, total marks of the first two tests, and total marks of the eight tests are in a geometric progression.
Question 18
If Ravi scored 4 marks in the first test, how many marks did Sumana score in the third test?
correct answer:-2
Instruction for set 1:
Read the following scenario and answer the THREE questions that follow.
Comprehension:
In an 8-week course, a professor administered a test at the end of each week. Each of the eight tests was scored out of 4 marks, and a student could only receive a non-negative integer score.
Two students, Ravi and Sumana, took the eight tests.
In the first test, Ravi and Sumana scored the same marks. From the second to eighth tests, Ravi scored the exact same non-zero marks. Sumana scored the same marks as Ravi from the fifth test onwards. Ravi’s total marks in the first three tests was the same as Sumana’s total marks in the first two tests. Also, Sumana’s marks in the first test, total marks of the first two tests, and total marks of the eight tests are in a geometric progression.
Question 19
If Ravi scored 1 mark in the second test, what is the maximum possible value of Sumana’s total marks in all the eight tests together?
correct answer:-3
Instruction for set 2:
Read the following scenario and answer the THREE questions that follow.
Comprehension:
GadRev is a firm that reviews different latest gadgets through a team of four reviewers (R1, R2, R3, and R4). Recently the reviewers reviewed four different tech gadgets (A, B, C, and D) on a scale of 1 to 5 (all integer values) where 1 denotes poor and 5 denotes excellent. These review ratings were then tabulated. However, due to a technical glitch, some of these ratings got deleted. The average rating given by each reviewer, and the average rating given to each gadget were earlier communicated to the team management in a separate email and hence can be useful to retrieve the deleted ratings. The available ratings along with the average ratings are represented in the following table:
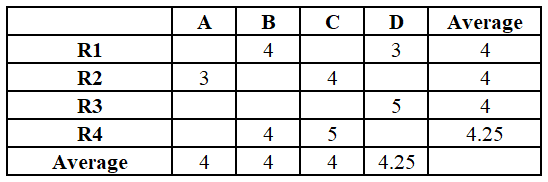
Question 20
What rating provided by Reviewer R1 to Gadget A can help determining the remaining ratings uniquely?
correct answer:-2

