A straight line $$L_1$$ has the equation $$y = k(x - 1)$$, where k is some real number. The straight line $$L_1$$ intersects another straight line $$L_2$$ at the point (5, 8).
If $$L_2$$ has a slope of 1, which of the following is definitely FALSE?

Given that the equation of line $$L_1$$ is $$y = k(x - 1)$$ and it intersects line $$L_2$$ at (5, 8).

So, the point (5, 8) must satisfy the equation of line $$L_1$$

We get $$8=k\left(5-1\right)$$

or $$k=2$$

Hence, the equation of line $$L_1$$ is $$y = 2(x - 1)$$ . . . (1)

Now, $$L_2$$ has a slope of 1 

Using slope form, the equation of line is $$y=mx+c$$, where $$m$$ is the slope and $$c$$ is the y-intercept

So, the equation of line $$L_2$$ is $$y=x+c$$

Now, as it passes through the point (5, 8), the equation must satisfy

Hence, $$8=5+c$$

or, $$c=3$$

Hence, the equation of line $$L_2$$ is $$y=x+3$$ . . . (2)

Plotting both lines on the graph, we get

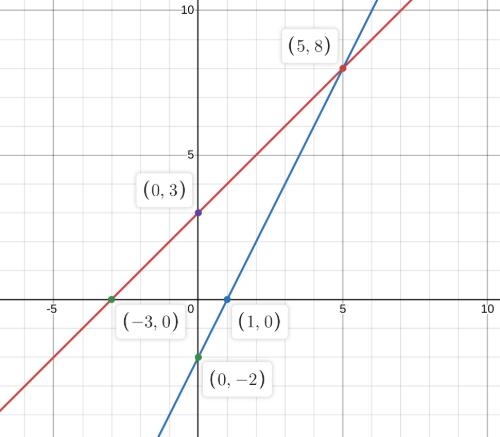
From the graph we can clearly see that the distance between the y-intercepts of the two lines is 5 not 6. 

Hence, the statement the distance between the y-intercepts of the two lines is 6 is definitely false.