A soild trophy, consisting of two parts, has been designed in the following manner: the bottom part is a frustum of a cone with the bottom radius 30 cm, the top radius 20 cm, and height 40 cm, while the top part is a hemisphere with radius 20 cm. Moreover, the flat surface of the hemisphere is the same as the top surface of the frustum.
If the entire trophy is to be gold-plated at the cost of Rs. 40 per square cm, what would the cost for gold-plating be closest to?

According to the question, we have the following figure:

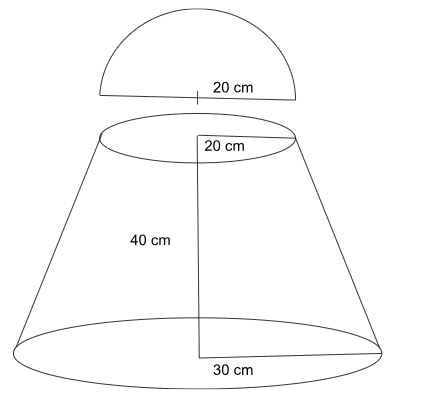
According to the question, we have a frustrum and a semisphere with flat surface and we need to find the curved surface area of the frustrum along with the curved surface area of the hemisphere and the bottom flat area of the frustrum. 

Curved surface area of the Frustrum = $$\pi\ \times\left(r_1+r_2\right)\times l$$

Here, r1 and r2 refers to the two different radii and l refers to the slant height. 

$$l=\sqrt{h^2+\left(r_1-r_2\right)^2}$$

$$l=\sqrt{1600+100}=\sqrt{1700}=10\sqrt{17}$$

Hence, curved surface area of the frustrum = $$\pi\ \times\left(20+30\right)\times10\sqrt{17}$$

$$\pi\ \times50\times10\sqrt{17}$$

$$500\sqrt{17}\pi\ $$

Now, curved surface area of the hemisphere = $$2\pi r^2=2\times\pi\ \times\ \left(20\right)^2\ =\ 800\pi\ $$

And the flat bottom area of the frustrum = $$\pi r^2=\pi\ \times\left(30\right)^2=900\pi\ $$

Hence, the total surface area of the trophy =$$500\sqrt{17}\pi\ +\ 800\pi\ +\ 900\pi\ =500\sqrt{17}\pi\ +\ 1700\pi\ $$

The cost of gold coating is Rs. 40 per square cm

Hence, the total cost of coating = $$40\times\ \left(500\sqrt{17}\pi\ +\ 1700\pi\ \right)$$

$$40\times\ \dfrac{22}{7}\times\ \left(500\sqrt{17}\ +\ 1700\ \right)$$

$$40\times\ \dfrac{22}{7}\times\ \left(2061.55\ +\ 1700\ \right)$$

$$40\times\ \dfrac{22}{7}\times\ 3761.55=Rs.\ 4,72,880.571\ \approx\ Rs.\ 4,73,000$$