An industrial robot manufacturing company is tasked to design humanoid robots to be used in warehouses where the robots need to pick items from a stack of shelves. The height of the topmost shelf from the ground is 7 feet. To operate, the robot has to move on a track, running parallel to the stack of shelves. The track is fixed 1 foot away from the base of the stack of shelves. Further, the robot cannot raise its arms by more than 60° from the horizontal plane.
If the robot’s arms are attached to its shoulder, what should be the minimum height of the robot from the ground to the shoulder for its arms to reach the topmost shelf?

According to the question, we can draw the following table:

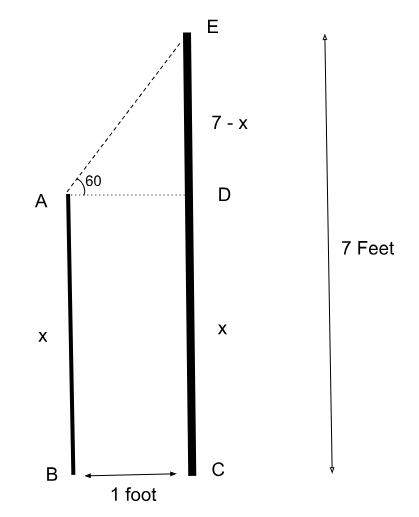
Here, EC refers to the shelf which is 7 feet and AB refers to the height of the robot. Here, AE reflects the hand of the robot. Since we need to find the minimum possible height, we need to maximize the length of the hands of the robot. The hands of the robot can be tilted to the maximum angle of 60, hence, we will assume that the hands of the robot tilt to exactly $$60^{\circ\ }$$.

Let the height of the robot i.e. AB be $$x$$ feet.

Now, we need to find the value of x. 

Since, BC = 1 foot, AD is also 1 foot. 

In triangle ADE, $$\tan\ 60^{\circ\ }=\dfrac{ED}{AD}$$

$$\tan\ 60^{\circ\ }=\dfrac{7-x}{1}$$

$$\sqrt{3}=\dfrac{7-x}{1}$$

$$x=7-\sqrt{3}$$