If Ravi scored 4 marks in the first test, how many marks did Sumana score in the third test?

According to the set, there are 8 tests and each test can have a maximum of 4 marks so any student can get a maximum of 32 marks. 

Now, the number of marks received by any student in a test can be 0/1/2/3/4.

We are given information about two students, Ravi and Sumana. 

In the first test, they both scored the same marks. Let the marks scored by both is $$x$$.

Further, from the second to eighth tests, Ravi scored the exact same non-zero marks. Let the marks scored by Ravi from second to eighth test is $$y$$ where y can be 1/2/3/4. Also, Sumana scored the same marks as Ravi from the fifth test onwards.

With this, we get the following table:

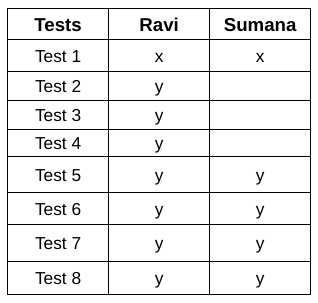
Ravi’s total marks in the first three tests was the same as Sumana’s total marks in the first two tests.

Let the marks of Sumana in the second test be $$z$$.

We are given that, $$x\ +\ 2y=x+z$$

Therefore, we can say, z = 2y.

We don't have any other information about their marks in specific tests so let the marks of Sumana in test 3 and test 4 be $$a$$ and $$b$$ respectively. 

With this, we have:

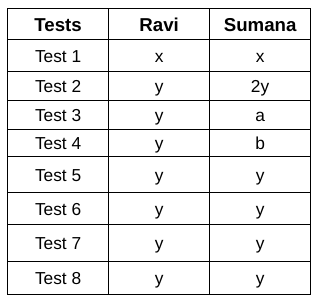
At last, we are given that Sumana’s marks in the first test, total marks of the first two tests, and total marks of the eight tests are in a geometric progression.

i.e. x, (x + 2y) and (x + a + b + 6y) are in a geometric progression. 

With this, we can infer that x can't be 0 as if x is 0, any number multiplied with it will be 0 and (x+2y) and (x + a + b + 6y) can't be in a geometric progression.

Hence, x can be 1 / 2 / 3 / 4.

Let's try to make all possible geometric progression with this information:

1. (1, 3, 9) when x = 1, y = 1 and a + b = 2

2. (2, 4, 8) when x = 2, y = 1 and a + b = 0

3. (2, 6, 8) when x = 2, y = 2 and a + b = 4

4. (4, 8, 16) when x = 4, y = 2 and a + b = 0

According to the question, if Ravi scored 4 marks in the first test i.e. if x = 4, the possible case is case 4,

Hence, sumana scored $$a$$ marks in the third test and we know that in case 4, a + b = 0. Hence, both $$a$$ and $$b$$ are 0.