A farmer has a quadrilateral parcel of land with a perimeter of 700 feet. Two opposite angles of that parcel of land are right angles, while the remaining two are not. The farmer wants to do organic farming on that parcel of land. The cost of organic farming is Rs. 400 per square foot.
Consider the following two additional pieces of information:
I. The length of one of the sides of that parcel of land is 110 feet.
II. The distance between the two corner points where the non-perpendicular sides of that parcel of land intersect is 255 feet.
To determine the amount of money the farmer needs to spend to do organic farming on the entire parcel of land, which of the above additional pieces of information is/are MINIMALLY SUFFICIENT?

Considering statement 1: We can only get the length of one of the sides of the land. But that is not sufficient to get the area.

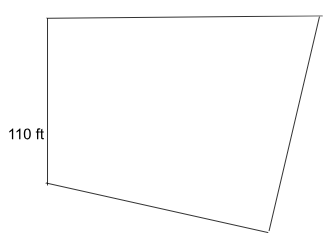
Considering statement 2: 

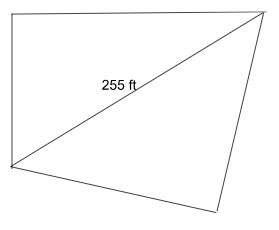
We are given the diagonal length.

With this information and the perimeter, it is not possible to find the area of land.

Considering both 1 and 2 statements.

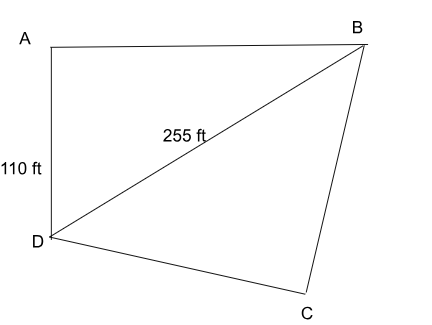
Now, we have two right-angle triangles. We know the hypotenuse of both triangles.

$$AB^2+AD^2=BD^2$$

$$110^2+AB^2= 255^2$$

AB$$\approx\ $$230

Let DC = x, BC = 700 - 110-230-x = 360-x.

$$x^2+(360-x)^2 = 255^2$$

Upon solving this we get x = 180$$\pm\frac{15}{\sqrt{2}}$$

360-x = 180$$\pm\frac{15}{\sqrt{2}}$$

Area of triangle ABD = $$\frac{1}{2}\cdot110\cdot230\ =\ 12650$$

Area of triangle BDC = $$\frac{1}{2}\left(180+\frac{15}{\sqrt{2}}\right)\left(180-\frac{15}{\sqrt{2}}\right)=16143.75$$

So, total area = 12650+16143.75 = 28793.75

Cost = 28793.75*400 = Rs. 11517500.

So, option C is the answer, as both statements 1 and 2 are required and sufficient to answer the question.