If $$\log_4m + \log_4n = \log_2(m + n)$$ where m and n are positive real numbers, then which of the following must be true?
XAT 2021 Question Paper - QUANT
For the following questions answer them individually
Solution
Share
$$\log_4mn=\log_2(m+n)$$
$$\sqrt{\ mn}=(m+n)$$
Squarring on both sides
$$m^2+n^2+mn\ =\ 0$$
Since m, n are positive real numbers, no value of m and n satisfy the above equations.
Mr. Jose buys some eggs. After bringing the eggs home, he finds two to be rotten and throws them away. Of the remaining eggs, he puts five-ninth in his fridge, and brings the rest to his mother’s house. She cooks two eggs and puts the rest in her fridge. If her fridge cannot hold more than five eggs, what is the maximum possible number of eggs bought by Mr. Jose?
Solution
Let the number of eggs bought = 9x+2
number of eggs left after throwing away 2 = 9x
number of eggs kept in fridge = 5x
number of eggs brought to his mothers' house = 4x
number of eggs left after cooking 2 which are kept in fridge = 4x-2
Given, 4x-2 <=5
=> x$$\le\frac{7}{4}$$
Hence the max value of x is 1
Max number of eggs bought = 11
Mohan has some money (₹M) that he divides in the ratio of 1:2. He then deposits the smaller amount in a savings scheme that offers a certain rate of interest, and the larger amount in another savings scheme that offers half of that rate of interest. Both interests compound yearly. At the end of two years, the total interest earned from the two savings schemes is ₹830. It is known that one of the interest rates is 10% and that Mohan deposited more than ₹1000 in each saving scheme at the start. What is the value of M?
Solution
Let the total amount be 3x
Case 1:
Smaller amount = x, rate of interest = 10
Larger amount = 2x, rate of interest = 5
Total amount received at the end of two years( smaller amount) = $$x\left(1+\frac{10}{100}\right)^2\ =\ 1.21x$$. CI = 0.21x
Total amount received at the end of two years( larger amount) = $$2x\left(1+\frac{5}{100}\right)^2\ =\ 2.205x$$ CI = 0.205x
Given, 0.21x + 0.205x = 830
=> x = 2000
2x= 4000
Case 2:
Smaller amount = x, rate of interest = 20
Larger amount = 2x, rate of interest = 10
Total amount received at the end of two years( smaller amount) = $$x\left(1+\frac{20}{100}\right)^2\ =\ 1.44x$$. CI = 0.44x
Total amount received at the end of two years( larger amount) = $$2x\left(1+\frac{10}{100}\right)^2\ =\ 2.42x$$ CI = 0.42x
Given, 0.44x+0.42x = 830
=> x = 965.11 which is not valid since it should be greater than 1000
A small store has five units of a new phone model in stock: two white, two black, and one red. Three customers arrive at the shop to buy a unit each. Each one has a pre- determined choice of the colour and will not buy a unit of any other colour. All the three customers are equally likely to have chosen any of the three colours. What is the probability that the store will be able to satisfy all the three customers?
Solution
Number of white phones = 2
Number of black phones = 2
Number of red phones = 1
customer 1 will have 3 choices
customer 2 will have 3 choices
customer 3 will have 3 choices
Hence total choices = 3 x 3 x 3 = 27
The cases not possible = BBB, RRR,WWW, RRB,RBR,BRR, RRW,RWR, WRR
Possible cases = 18
Probability = 18/27 = 2/3
At any point of time, let x be the smaller of the two angles made by the hour hand with the minute hand on an analogue clock (in degrees). During the time interval from 2:30 p.m. to 3:00 p.m., what is the minimum possible value of x?
Solution
The difference between the hour and minute hand of a clock is given by $$\left|30H-5.5m\right|$$. Here H is the current hour and m represents the number of completed minutes in the current hour.
In the given time frame of 2: 30 to 3: 00 pm.
At 2 : 30 pm the angle = $$\left|30\cdot2-5.5\cdot30\right|\ =\ 105\ \deg rees$$
At 3: 00 pm the angle = $$\left|30\cdot3-5.5\cdot0\right|\ =\ 90\ \deg rees$$
The function of $$\left|30\cdot H-5.5\cdot m\right|\ =\ $$ constantly increases as the value of m increases from 31, 32................ 59.
Because of the modulus function, the net value of the function remains positive
Between 2: 30 to 2: 59 the angle is constantly increasing. The minimum value is 2: 30 which is equal to 105 degrees which is greater than the 90 degrees when the time is 3: 00.
Hence 90 degrees is the minimum angle.
One third of the buses from City A to City B stop at City C, while the rest go non-stop to City B. One third of the passengers, in the buses stopping at City C, continue to City B, while the rest alight at City C. All the buses have equal capacity and always start full from City A. What proportion of the passengers going to City B from City A travel by a bus stopping at City C?
Solution
Let us assume there are three buses, each carrying 30 passengers.
Now it is given that one-third of the buses from City A to City B stop at City C, while the rest go non-stop to City B. This means that one bus stops at C while two buses go directly to B. This means that $$2\times 30=60$$ passengers directly reach to B.
For the buses that stops at C, One-third of the passengers continue to City B, that is 10 passengers in each bus continue to city B, while the rest alight at City C. Since there is only one bus which stops at city C, this means that $$1\times 20=20$$ passengers alight at C, while $$1\times 10=10$$ passengers travel from city C to city B.
We are asked what proportion of the passengers going to City B from City A travel by a bus stopping at City C. So, in total, we can see the total number of passengers who are travelling to City B is 70, while the number of passengers travelling by the buses that stop at City C is 10.
So, the proportion of the passengers going to City B from City A who travel by a bus stopping at City C = $$\dfrac{10}{70}=\dfrac{1}{7}$$
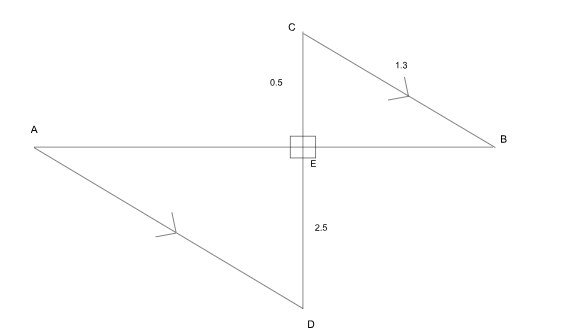
Rajesh, a courier delivery agent, starts at point A and makes a delivery each at points B, C and D, in that order. He travels in a straight line between any two consecutive points. The following are known: (i) AB and CD intersect at a right angle at E, and (ii) BC, CE and ED are respectively 1.3 km, 0.5 km and 2.5 km long. If AD is parallel to BC, then what is the total distance (in km) that Rajesh covers in travelling from A to D?
Solution
Based on the information, the following figure can be obtained.
Given, CE=0.5, BC = 1.3 and ED=2.5
Triangle CEB is a right-angled triangle => EB = 1.2
$$\triangle\ $$ ECB is similar to $$\triangle\ $$ EDA
EB/EC = AE/ED => AE = 6
Hence total distance travelled = AB + BC + CD = 7.2 + 1.3 + 3 = 11.5km
Let $$f(x) = \frac{x^2 + 1}{x^2 - 1}$$ if $$x \neq 1, -1,$$ and 1 if x = 1, -1. Let $$g(x) = \frac{x + 1}{x - 1}$$ if $$x \neq 1,$$ and 3 if x = 1.
What is the minimum possible values of $$\frac{f(x)}{g(x)}$$ ?
Solution
$$\frac{f\left(x\right)}{g\left(x\right)}=\frac{\left(x^2+1\right)}{x^2-1}\cdot\frac{\left(x-1\right)}{x+1}=\frac{\left(x^2+1\right)}{\left(x+1\right)^2}$$
This function is definitely greater than 0
$$let\ y=\frac{\left(x^2+1\right)}{\left(x+1\right)^2}$$
=> $$x^2\left(y-1\right)+2yx+\left(y-1\right)=0$$ which is quadratic in x
Disctiminant should be greater than 0
$$4y^2-4\left(y-1\right)^2\ge0$$
=> y>=1/2
When x =1, f(x)/g(x) = 1/3
Hence either the value should be greater than 1/2 or should be equal to 1/3
Swati can row a boat on still water at a speed of 5 km/hr. However, on a given river, it takes her 1 hour more to row the boat 12 km upstream than downstream. One day, Swati rows the boat on this river from X to Y, which is N km upstream from X. Then she rows back to X immediately. If she takes at least 2 hours to complete this round trip, what is the minimum possible value of N?
Solution
Let the speed of the stream be x
$$\frac{12}{5-x}=\frac{12}{5+x}+1$$
The value of x satisfying the above equation is 1
Now,
$$\frac{N}{5+1}+\frac{N}{5-1}\ge2$$
$$\frac{2N+3N}{12}\ge2$$
=> $$N\ge4.8$$
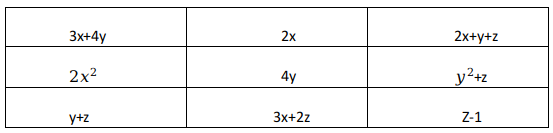
Rahul has just made a $$3 \times 3$$ magic square, in which, the sum of the cells along any row, column or diagonal, is the same number N. The entries in the cells are given as expressions in x, y, and Z. Find N?
Solution
Sum of 3rd row = sum of 2nd column
=> 2x+4y = y+2z-1
=> 2x+3y-2z= -1 ------- (A)
Sum of diagonals are also equal
=> 3x+4y+z-1 = y+z+2x+y+z
=> x+2y-z=1 -----(B)
Solving A and B we get y= 3
Putting it in A, we get x-z = -5 ----- (C)
Sum of 1st row = sum of 2nd column
5x+5y+z = 3x+4y+2z
=> 2x +y - z =0
Since y=3, 2x-z = -3 ------ (D)
Solving C and D we get x=2 and z=7
Hence N = 36
On the bank of the pristine Tunga river, a deer and a tiger are joyfully playing with each other. The deer notices that it is 40 steps away from the tiger and starts running towards it. At the same time, the tiger starts running away from the deer. Both run on the same straight line. For every five steps the deer takes, the tiger takes six. However, the deer takes only two steps to cover the distance that the tiger covers in three. In how many steps can the deer catch the tiger?
Solution
Let speed of deer = 5steps/second and speed of tiger = 6 steps/sec
Let deer cover 1 m in a step => tiger covers 2/3 m in a step
Hence speed of deer = 5m/s and spped of tiger = 6 x 2/3 m/s = 4m/s
Hence time taken by a deer to catch tiger = 40 seconds
Distance travelled by deer in 40 seconds = 5 x 40 =200 steps
Read the following scenario and answer the three questions that follow.
A company awards incentives to its employees for successful project performances. It rates successful project performance in categories A*, A, B, and C. Employees, in solo projects rated A*, A, B, and C, are awarded incentives ₹6 lakh, ₹5 lakh, ₹3 lakh, and ₹1 lakh respectively. When a project has multiple team members, the following scheme is used to award the incentives:
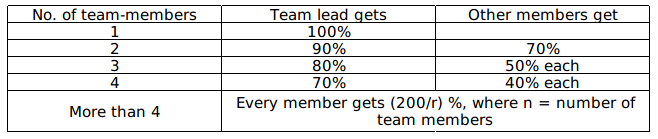
For example, for a project rated A, with three members, the team lead gets ₹4 lakh, and the other team members get ₹2.5 lakh each. A project always has a single team lead.
Six employees: Altaf, Bose, Chakrabarthi, Dipa, Ernie, and Fatima receive a total of ₹45 lakh in incentives by participating in a total of eight different projects that does not involve any other person. Not all six employees are involved in all eight projects.
The following are additionally known about these eight projects:
1. One project involves all six employees. Four projects involve three each, and the rest, two each.
2. Exactly three projects are rated C, for which a total of ₹4.8 lakh is paid.
3. Only one project is rated A*.
What BEST is known about the team compositions for the projects rated C?
Solution
Total percentage incentive when number of team members = 1 = 100%
Total percentage incentive when the number of team members =2 =160%
Total percentage incentive when the number of team members =3=180%
Total percentage incentive when the number of team members =4= 190%
Total percentage incentive when the number of team members >4 = 200%
From 1, Number of people in 8 different projects = 6, 3, 3,3,3, 2,2,2 respectively
From 2, Given, exactly three projects are rated C and 4.8 lakh is paid in total
A minimum of 3 lakhs has to be paid for rating C => 3 *1.6 = 4.8lakhs => All 2 member teams have been rated C
From 3, one project has been rated A*. Let that project be handled by the team of 3 members => Incentives = 180% of 6 = 10.8 lakh
Now remaining 6,3,3,3 should be either rated A or B and the total incentives should be equal to 45 - 10.8-4.8 = 29.4 lakhs
Let us assume 6 has been rated B => Incentives = 200% of 3 = 6 lakhs
The remaining 23.4 lakhs should come from 180%. $$\frac{23.4}{1.8}=13\ lakhs$$
Hence the remaining 3,3,3 can be rated as A, A, B
Hence final ratings are and total payouts are
6 - B - 6lakhs
3- A - 9 lakhs
3-A - 9 lakhs
3-B - 5.4 lakhs
3-A* - 10.8lakhs
2-C - 1.6 lakhs
2-C - 1.6 lakhs
2-C - 1.6 lakhs
What BEST is known about the team composition for the project rated A*?
Solution
Total percentage incentive when number of team members = 1 = 100%
Total percentage incentive when the number of team members =2 =160%
Total percentage incentive when the number of team members =3=180%
Total percentage incentive when the number of team members =4= 190%
Total percentage incentive when the number of team members >4 = 200%
From 1, Number of people in 8 different projects = 6, 3, 3,3,3, 2,2,2 respectively
From 2, Given, exactly three projects are rated C and 4.8 lakh is paid in total
A minimum of 3 lakhs has to be paid for rating C => 3 *1.6 = 4.8lakhs => All 2 member teams have been rated C
From 3, one project has been rated A*. Let that project be handled by the team of 3 members => Incentives = 180% of 6 = 10.8 lakh
Now remaining 6,3,3,3 should be either rated A or B and the total incentives should be equal to 45 - 10.8-4.8 = 29.4 lakhs
Let us assume 6 has been rated B => Incentives = 200% of 3 = 6 lakhs
The remaining 23.4 lakhs should come from 180%. $$\frac{23.4}{1.8}=13\ lakhs$$
Hence the remaining 3,3,3 can be rated as A, A, B
Hence final ratings are and total payouts are
6 - B - 6lakhs
3- A - 9 lakhs
3-A - 9 lakhs
3-B - 5.4 lakhs
3-A* - 10.8lakhs
2-C - 1.6 lakhs
2-C - 1.6 lakhs
2-C - 1.6 lakhs
Total amount of money paid for projects rated A (in lakhs of Rupees) is:
Solution
Total percentage incentive when number of team members = 1 = 100%
Total percentage incentive when the number of team members =2 =160%
Total percentage incentive when the number of team members =3=180%
Total percentage incentive when the number of team members =4= 190%
Total percentage incentive when the number of team members >4 = 200%
From 1, Number of people in 8 different projects = 6, 3, 3,3,3, 2,2,2 respectively
From 2, Given, exactly three projects are rated C and 4.8 lakh is paid in total
A minimum of 3 lakhs has to be paid for rating C => 3 *1.6 = 4.8lakhs => All 2 member teams have been rated C
From 3, one project has been rated A*. Let that project be handled by the team of 3 members => Incentives = 180% of 6 = 10.8 lakh
Now remaining 6,3,3,3 should be either rated A or B and the total incentives should be equal to 45 - 10.8-4.8 = 29.4 lakhs
Let us assume 6 has been rated B => Incentives = 200% of 3 = 6 lakhs
The remaining 23.4 lakhs should come from 180%. $$\frac{23.4}{1.8}=13\ lakhs$$
Hence the remaining 3,3,3 can be rated as A, A, B
Hence final ratings are and total payouts are
6 - B - 6lakhs
3- A - 9 lakhs
3-A - 9 lakhs
3-B - 5.4 lakhs
3-A* - 10.8lakhs
2-C - 1.6 lakhs
2-C - 1.6 lakhs
2-C - 1.6 lakhs
Read the following scenario and answer the three questions that follow.
A quick survey at the end of a purchase at buyagain.com asks the following three questions to each shopper:
1. Are you shopping at the website for the first time? (YES or NO)
2. Specify your gender: (MALE or FEMALE)
3. How satisfied are you? (HAPPY, NEUTRAL or UNHAPPY)
240 shoppers answer the survey, among whom 65 are first time shoppers. Furthermore:
i. The ratio of the numbers of male to female shoppers is 1 : 2 while the ratio of the numbers of unhappy, happy and neutral shoppers is 3 : 4 : 5
ii. The ratio of the numbers of happy first-time male shoppers, happy returning male shoppers, unhappy female shoppers, neutral male shoppers, neutral female shoppers and happy female shoppers is 1 : 1 : 4 : 4 : 6 : 6
iii. Among the first-time shoppers, the ratio of the numbers of happy male, neutral male, unhappy female and the remaining female shoppers is 1 : 1 : 1 : 2, while the number of happy first-time female shoppers is equal to the number of unhappy first-time male shoppers
What is the number of happy male shoppers?
Solution
From the given data the following table can be created:
Hence the value of x=10
Which among the following is the lowest?
Solution
From the given data the following table can be created:
Hence the value of x=10
From the given options, number of neutral first time female shoppers are the least
Which among the following cannot be determined uniquely?
Solution
From the given data the following table can be created:
Hence the value of x=10
All the values can be uniquely determined
For the following questions answer them individually
The six faces of a wooden cube of side 6 cm are labelled A, B, C, D, E and F respectively. Three of these faces A, B, and C are each adjacent to the other two, and are painted red. The other three faces are not painted. Then, the wooden cube is neatly cut into 216 little cubes of equal size. How many of the little cubes have no sides painted?
Solution
Since A, B and C are adjacent faces. If we remove them, the resultant solid will also be a cube with side 5.
Hence total number of cubes unpainted = $$5^3$$ = 125
ABC is a triangle with integer-valued sides AB = 1, BC >1, and CA >1. If D is the mid-point of AB, then, which of the following options is the closest to the maximum possible value of the angle ACD (in degrees)?
Solution
We will try to maximize the value of the angle ACD:
For a fixed triangle ABC, the angle ACD can be maximized when we take the median CD to be perpendicular to AB and the value of AC is as small as possible, so that the sine of angle ACD, and hence, the angle ACD itself if maximized, as the value of AD is fixed at half of AB at 0.5.
Now, the least possible value of AC is 2. The triangle will be of sides (1,2,2).
Value of sin(ACD)=$$\frac{0.5}{2}=0.25$$
$$\angle\ ACD=\sin^{-1}\left(0,25\right)=14.78\approx\ 15.$$
Find z, if it is known that:
a: $$-y^2 + x^2 = 20$$
b: $$y^3 - 2x^2 - 4z \geq -12$$ and
c: x, y and z are all positive integers
Solution
Since $$x^2-y^2=20$$ and x,y,z are positive integers,
(x+y)*(x-y) = 20, Hence x-y, x+y are factors of 20.
Since x, y are positive integers, x+y is always positive, and for the product of (x+y)*(x-y) to be positive x-y must be positive.
x, y are positive integers and x-y is positive x must be greater than y.
The possible cases are : (x+y = 10, x-y = 2), (x+y = 5, x-y = 4).
The second case fails because we get x =9/2, y = 1/2 but x, y are integral values
For case one x = 6, y = 4.
$$y^3 - 2x^2 - 4z \geq -12$$
Substituting the values of x and y, we have :
64 - 72 - 4*z $$\ge\ -12$$
-8 - 4*z $$\ge\ -12$$
z$$\le\ 1$$
Since x, y, z are positive integers, the only possible value for z is 1.
An encryption system operates as follows:
Step 1. Fix a number k $$(k \leq 26)$$.
Step 2. For each word, swap the first k letters from the front with the last k letters from the end in reverse order. If a word contains less than 2k letters, write the entire word in reverse order.
Step 3. Replace each letter by a letter k spaces ahead in the alphabet. If you cross Z in the process to move k steps ahead, start again from A.
Example: k = 2: zebra --> arbez --> ctdgb.
If the word “flight” becomes “znmorl” after encryption, then the value of k:
Solution
Flight become znmorl
Let's assume $$k>3$$
So flight will become thgilf -> znmrol. Hence the value of k will be 6
Read the following scenario and answer the three questions that follow.
The following plot describes the height (in cm), weight (in kg), age (in years) and gender (F for female, M for male) of 20 patients visiting a hospital.
A person’s body mass index (BMI) is calculated as weight (in kg) divided by squared height (measured in square metres). For example, a person weighing 100 kg and of height 100 cm (1m) will have a BMI of 100. A person with BMI less than or equal to 18.5 is considered as underweight, above 18.5 but less than or equal to 25 as normal weight, above 25 but less than or equal to 30 as overweight, and above 30 as obese.
The average age of the female patients who weigh 50 kg or above is approximately
Solution
There are 5 ladies whose weights are 50 or above
There ages are 50,50, 70,60 and 80
Average = 310/5 = 62
The highest BMI among all patients is approximately
Solution
For the highest BMI, weight should be as high as possible and height as little as possible.
Hence it is possible with the person with a weight of 69 kg and a height of 1.6m
His BMI will be $$\frac{69}{\left(1.6\right)^2}=27$$
The BMI of the oldest person considered as normal weight is approximately
Solution
The BMI of 1st oldest person= $$\frac{40}{\left(1.5\right)^2}=\ 17.77$$
The BMI of next oldest person = $$\frac{61}{\left(1.75\right)^2}=19.9$$
For the following questions answer them individually
The topmost point of a perfectly vertical pole is marked A. The pole stands on a flat ground at point D. The points B and C are somewhere between A and D on the pole. From a point E, located on the ground at a certain distance from D, the points A, B and C are at angles of 60, 45 and 30 degrees respectively. What is AB : BC : CD?
Solution
Let ED = $$\sqrt{\ 3}x$$
In triangle CDE, $$\tan\ 30\ =\ \frac{CD}{\sqrt{\ 3}x}$$ => CD = x
In triangle BDE, $$\tan\ 45\ =\ \frac{BD}{\sqrt{\ 3}x}$$ => BD = $$\sqrt{\ 3}x$$ => BC = $$\sqrt{\ 3}x\ -x$$
In triangle ADE, $$\tan\ 60\ =\ \frac{AD}{\sqrt{\ 3}x}$$ => AD = 3x => AB = $$3x\ -\ \sqrt{\ 3}x$$
AB : BC : CD = $$(3 - \sqrt 3) : (\sqrt 3 - 1) : 1$$
Two circles P and Q, each of radius 2 cm, pass through each other’s centres. They intersect at points A and B. A circle R is drawn with diameter AB. What is the area of overlap (in square cm) between the circles R and P?
Solution
We know that radius of circle P is 2 cm
Length of MO = 1 cm
radius of circle R = AO = $$\sqrt{\ 2^2-1^2}$$ = $$\sqrt{\ 3}$$
Area of overlap between the circle R and P(shaded region) = semi circle area of R + area of segment ANBOA
Area of segment ANBOA = area of sector ANBM - area of triangle AMB
= $$\frac{120}{360}\pi\ \left(2\right)^2$$ - $$\frac{1}{2}\left(1\right)\left(2\sqrt{\ 3}\right)$$
= $$\frac{4\pi}{3}-\sqrt{\ 3}$$
Area of overlap between circle R and P = $$\frac{\pi\ \left(\sqrt{\ 3}\right)^2}{2}$$+ $$\frac{4\pi}{3}-\sqrt{\ 3}$$
= $$\ \frac{\ 17\pi\ }{6}-\sqrt{\ 3}$$
Answer is option E.
Four friends, Ashish, Brian, Chaitra, and Dorothy, decide to jog for 30 minutes inside a stadium with a circular running track that is 200 metres long. The friends run at different speeds. Ashish completes a lap exactly every 60 seconds. Likewise, Brian, Chaitra and Dorothy complete a lap exactly every 1 minute 30 seconds, 40 seconds and 1 minute 20 seconds respectively. The friends begin together at the start line exactly at 4 p.m. What is the total of the numbers of laps the friends would have completed when they next cross the start line together ?
Solution
All the four friends will meet at the starting point after LCM(60,90,40,80) = 720 seconds.
Number of laps by A in 720 seconds = 12
Number of laps by B in 720 seconds = 8
Number of laps by C in 720 seconds = 18
Number of laps by D in 720 seconds = 9
Together they complete = 47 laps
Zahir and Raman are at the entrance of a dark cave. To enter this cave, they need to open a number lock. Raman sees a note on a rock: “ ... chest of pure diamonds kept for the smart one ... number has six digits ... second last digit is 2, third last is 4 ... divisible by all prime numbers less than 15 ...”. Excited, Zahir and Raman seek your help: which of these can be the first digit of the six-digit number that will help them open the lock?
Solution
Let the 6 digit number be _ _ _ 42_
It is divisible by 2,3,5,7,11,13
Since the number is divisible by both 2 and 5 the last digit of the number must be 0.
The number is also divisible by 3, 7, 11, and 13.
Hence the number must also be divisible by 7*11*13.
=7*11*13 = 1001.
A number which is a multiple of 1001 is of the form abcabc.
This is because abc*(1001) = abc*(1000+1) = abc000 + abc = abcabc.
Hence the number is 420420.
The first digit is 4.
