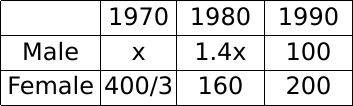CAT 2021 Slot 3 Quant Question Paper
For the following questions answer them individually
CAT 2021 Slot 3 Quant - Question 45
A shop owner bought a total of 64 shirts from a wholesale market that came in two sizes, small and large. The price of a small shirt was INR 50 less than that of a large shirt. She paid a total of INR 5000 for the large shirts, and a total of INR 1800 for the small shirts. Then, the price of a large shirt and a small shirt together, in INR, is
CAT 2021 Slot 3 Quant - Question 46
One day, Rahul started a work at 9 AM and Gautam joined him two hours later. They then worked together and completed the work at 5 PM the same day. If both had started at 9 AM and worked together, the work would have been completed 30 minutes earlier. Working alone, the time Rahul would have taken, in hours, to complete the work is
CAT 2021 Slot 3 Quant - Question 47
In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be
CAT 2021 Slot 3 Quant - Question 48
The number of distinct pairs of integers (m,n), satisfying $$\mid1+mn\mid<\mid m+n\mid<5$$ is:
789
456
123
0.-
Clear All
CAT 2021 Slot 3 Quant - Question 49
For a real number a, if $$\frac{\log_{15}{a}+\log_{32}{a}}{(\log_{15}{a})(\log_{32}{a})}=4$$ then a must lie in the range
CAT 2021 Slot 3 Quant - Question 50
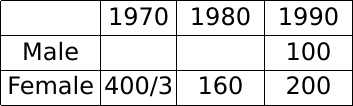
The total of male and female populations in a city increased by 25% from 1970 to 1980. During the same period, the male population increased by 40% while the female population increased by 20%. From 1980 to 1990, the female population increased by 25%. In 1990, if the female population is twice the male population, then the percentage increase in the total of male and female populations in the city from 1970 to 1990 is
CAT 2021 Slot 3 Quant - Question 51
Consider a sequence of real numbers, $$x_{1},x_{2},x_{3},...$$ such that $$x_{n+1}=x_{n}+n-1$$ for all $$n\geq1$$. If $$x_{1}=-1$$ then $$x_{100}$$ is equal to
CAT 2021 Slot 3 Quant - Question 52
The arithmetic mean of scores of 25 students in an examination is 50. Five of these students top the examination with the same score. If the scores of the other students are distinct integers with the lowest being 30, then the maximum possible score of the toppers is
789
456
123
0.-
Clear All
CAT 2021 Slot 3 Quant - Question 53
One part of a hostel’s monthly expenses is fixed, and the other part is proportional to the number of its boarders. The hostel collects ₹ 1600 per month from each boarder. When the number of boarders is 50, the profit of the hostel is ₹ 200 per boarder, and when the number of boarders is 75, the profit of the hostel is ₹ 250 per boarder. When the number of boarders is 80, the total profit of the hostel, in INR, will be
CAT 2021 Slot 3 Quant - Question 54
The cost of fencing a rectangular plot is ₹ 200 per ft along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is
CAT 2021 Slot 3 Quant - Question 55
A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is
789
456
123
0.-
Clear All
CAT 2021 Slot 3 Quant - Question 56
A tea shop offers tea in cups of three different sizes. The product of the prices, in INR, of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by INR 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes, in INR, is
789
456
123
0.-
Clear All
CAT 2021 Slot 3 Quant - Question 57
Mira and Amal walk along a circular track, starting from the same point at the same time. If they walk in the same direction, then in 45 minutes, Amal completes exactly 3 more rounds than Mira. If they walk in opposite directions, then they meet for the first time exactly after 3 minutes. The number of rounds Mira walks in one hour is
789
456
123
0.-
Clear All
CAT 2021 Slot 3 Quant - Question 58
If a certain weight of an alloy of silver and copper is mixed with 3 kg of pure silver, the resulting alloy will have 90% silver by weight. If the same weight of the initial alloy is mixed with 2 kg of another alloy which has 90% silver by weight, the resulting alloy will have 84% silver by weight. Then, the weight of the initial alloy, in kg, is
CAT 2021 Slot 3 Quant - Question 59
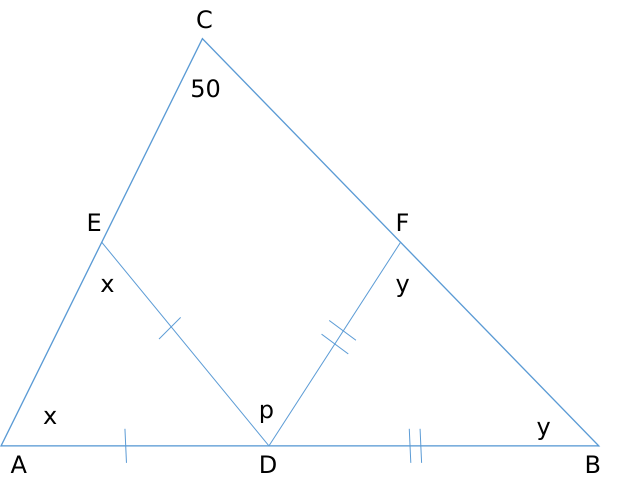
If a triangle ABC, $$\angle BCA=50^{0}$$. D and E are points on $$AB$$ and $$AC$$, respectively, such that $$AD=DE$$. If F is a point on $$BC$$ such that $$BD=DF$$, then $$\angle FDE$$, in degrees, is equal to
CAT 2021 Slot 3 Quant - Question 60
Bank A offers 6% interest rate per annum compounded half-yearly. Bank B and Bank C offer simple interest but the annual interest rate offered by Bank C is twice that of Bank B. Raju invests a certain amount in Bank B for a certain period and Rupa invests ₹ 10,000 in Bank C for twice that period. The interest that would accrue to Raju during that period is equal to the interest that would have accrued had he invested the same amount in Bank A for one year. The interest accrued, in INR, to Rupa is
CAT 2021 Slot 3 Quant - Question 61
If $$f(x)=x^{2}-7x$$ and $$g(x)=x+3$$, then the minimum value of $$f(g(x))-3x$$ is:
CAT 2021 Slot 3 Quant - Question 62
Anil can paint a house in 12 days while Barun can paint it in 16 days. Anil, Barun, and Chandu undertake to paint the house for ₹ 24000 and the three of them together complete the painting in 6 days. If Chandu is paid in proportion to the work done by him, then the amount in INR received by him is
789
456
123
0.-
Clear All
CAT 2021 Slot 3 Quant - Question 63
If n is a positive integer such that $$(\sqrt[7]{10})(\sqrt[7]{10})^{2}...(\sqrt[7]{10})^{n}>999$$, then the smallest value of n is
789
456
123
0.-
Clear All
CAT 2021 Slot 3 Quant - Question 64
A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is
789
456
123
0.-
Clear All
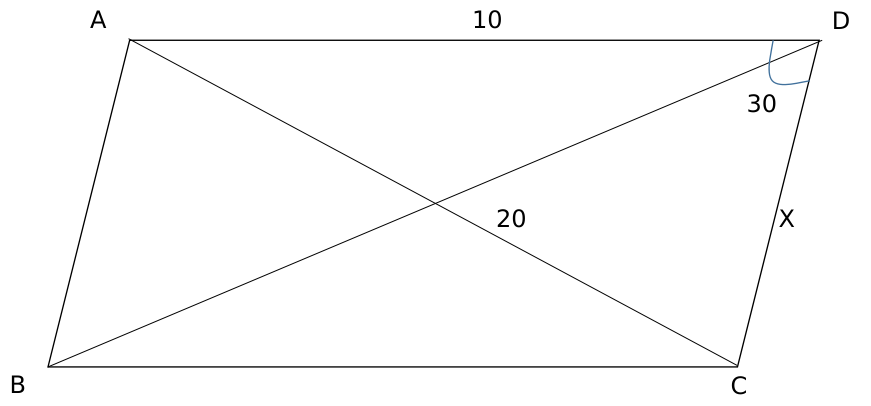
CAT 2021 Slot 3 Quant - Question 65
Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10cm and 20cm, respectively. If the angle $$\angle ADC$$ is equal to $$30^{0}$$ then the area of the parallelogram, in sq.cm is
CAT 2021 Slot 3 Quant - Question 66
If $$3x+2\mid y\mid+y=7$$ and $$x+\mid x \mid+3y=1$$ then $$x+2y$$ is:
Two Factor Authentication
Incase of any issue contact support@cracku.in