A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is

The question asks for the number of 4 digit numbers using only the digits 1, 2, and 3 such that the digits 2 and 3 appear at least once.

The different possibilities include :

Case 1:The four digits are ( 2, 2, 2, 3). Since the number 2 is repeated 3 times. The total number of arrangements are :

$$\frac{4!}{3!}$$ = 4.

Case 2: The four digits are 2, 2, 3, 3. The total number of four-digit numbers formed using this are :

$$\frac{4!}{2!\cdot2!}=\ 6$$

Case 3: The four digits are 2, 3, 3, 3. The number of possible 4 digit numbers are :

$$\frac{4!}{3!}$$ = 4

Case4: The four digits are 2, 3, 3, 1. The number of possible 4 digit numbers are :

$$\frac{4!}{2!}=\ 12$$

Case5: Using the digits 2, 2, 3, 1. The number of possible 4 digit numbers are :

$$\frac{4!}{2!}=\ 12$$

Case 6: Using the digits 2, 3, 1, 1. The number of possible 4 digit numbers are :

$$\frac{4!}{2!}=\ 12$$

A total of 12 + 12 + 12 + 4 + 6 + 4 = 50 possibilities.

Alternatively


  We have to form 4 digit numbers using 1,2,3 such that 2,3 appears at least once 
So the possible cases :

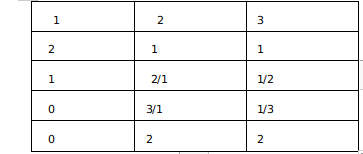
Now we get $$\frac{4!}{2!}\times\ 3$$= 36 ( When one digit is used twice and the remaining two once )
$$\frac{4!}{3!}\times\ 2$$ = 8 ( When 1 is used 0 times and 2 and 3 is used 3 times or 1 time )
$$\frac{4!}{2!\times\ 2!}=\ 6$$( When 2 and 3 is used 2 times each )
So total numbers = 36+8+6 =50