Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 65
Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10cm and 20cm, respectively. If the angle $$\angle ADC$$ is equal to $$30^{0}$$ then the area of the parallelogram, in sq.cm is
Solution
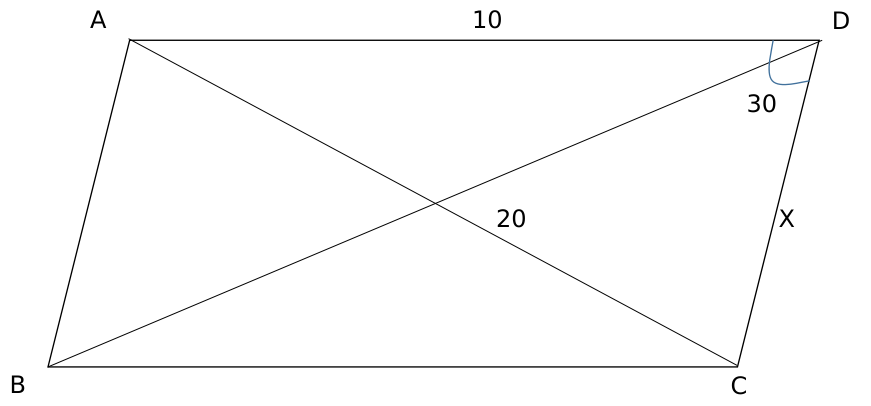
Applying cosine rule in triangle ACD,
$$100+X^2-2\times\ 10\times\ X\cos30=400$$
$$X^2-10X\sqrt{\ 3}-300=0$$
Solving, we get X = $$\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)$$
Hence, area = 10Xsin 30 = $$\frac{\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)10}{2}$$
= $$25(\sqrt{3}+\sqrt{15})$$
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
CAT Quant Questions | CAT Quantitative Ability
CAT Linear Equations QuestionsCAT Mensuration QuestionsCAT Time And Work QuestionsCAT Logarithms QuestionsCAT Percentages Questions
CAT DILR Questions | LRDI Questions For CAT
CAT Venn Diagrams QuestionsCAT Puzzles QuestionsCAT Games and Tournamnents QuestionsCAT Data Interpretation QuestionsCAT Truth Lie Concept Questions
