Question 59

If a triangle ABC, $$\angle BCA=50^{0}$$. D and E are points on $$AB$$ and $$AC$$, respectively, such that $$AD=DE$$. If F is a point on $$BC$$ such that $$BD=DF$$, then $$\angle FDE$$, in degrees, is equal to

Solution

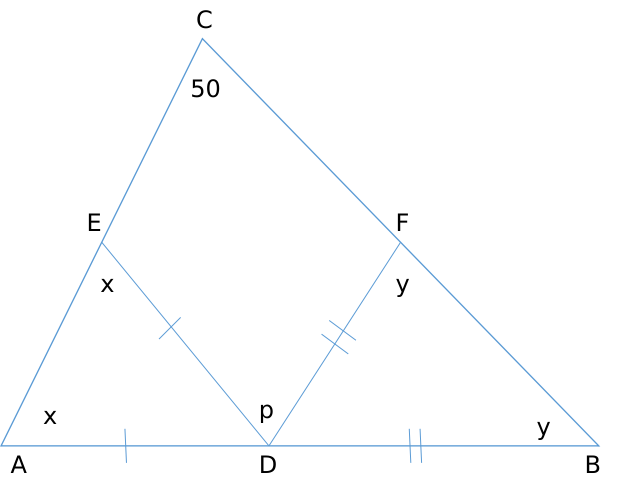
We need to find out p.

Angle ADE = 180 - 2x

Angle BDF = 180 - 2y

Now, 180 - 2y + p + 180 - 2x = 180 [Straight line = 180 deg]

p = 2x + 2y - 180

Also, x + y + 50 = 180 [Sum of the angles of triangle = 180]

x + y = 130

p = 260 - 180 = 80 degrees.

Share on Whatsapp Share on Whatsapp

Boost your CAT prep: Take All-India 3 free CAT mock tests with Video solutions

Video Solution

Click on the Email ☝️ to Watch the Video Solution

Your Doubts

Ask a Doubt (know more)

Drop Your File Here!

Create a FREE account and get:

All Quant CAT complete Formulas and shortcuts PDF
38+ CAT previous year papers with video solutions PDF
5000+ Topic-wise Previous year CAT Solved Questions for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Probability, Combinatorics Questions CAT Logarithms, Surds and Indices Questions CAT Simple Interest Compound Interest Questions CAT Venn Diagrams Questions CAT Quadratic Equations Questions

CAT DILR Questions | LRDI Questions For CAT

CAT Maxima-Minima Questions CAT Arrangement Questions CAT Selection With Condition Questions CAT Routes And Networks Questions CAT Table based DI Sets Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Vocabulary Questions CAT Para Summary Questions CAT Verbal Ability Questions CAT Para Jumbles Questions CAT Miscellaneous Questions

If a triangle ABC, $$\angle BCA=50^{0}$$. D and E are points on $$AB$$ and $$AC$$, respectively, such that $$AD=DE$$. If F is a point on $$BC$$ such that $$BD=DF$$, then $$\angle FDE$$, in degrees, is equal to

Video Solution

Your Doubts

Drop Your File Here!

CAT Quant Questions | CAT Quantitative Ability

CAT DILR Questions | LRDI Questions For CAT

CAT Verbal Ability Questions | VARC Questions For CAT

Also Read

Related Formulas With Tests

CAT 2021 QA Slot 3 Question

If a triangle ABC, $$\angle BCA=50^{0}$$. D and E are points on $$AB$$ and $$AC$$, respectively, such that $$AD=DE$$. If F is a point on $$BC$$ such that $$BD=DF$$, then $$\angle FDE$$, in degrees, is equal to

Video Solution

Your Doubts

Drop Your File Here!

CAT Quant Questions | CAT Quantitative Ability

CAT DILR Questions | LRDI Questions For CAT

CAT Verbal Ability Questions | VARC Questions For CAT

Also Read

Free CAT Quant Questions

Related Formulas With Tests

Login to your Cracku account

Hello! 👋

Ready to Unlock Your Success?

Please Enter Your OTP

Please enter the following details

Create a free Cracku account

Get Started with 5000+ Free CAT Questions & Mock Tests with Detailed Solutions!