The number of distinct pairs of integers (m,n), satisfying $$\mid1+mn\mid<\mid m+n\mid<5$$ is:

Let us break this up into 2 inequations [ Let us assume x as m and y as n ]

| 1 + mn | < | m + n |

| m + n | < 5

Looking at these expressions, we can clearly tell that the graphs will be symmetrical about the origin.

Let us try out with the first quadrant and extend the results to the other quadrants.

We will also consider the +X and +Y axes along with the quadrant.

So, the first inequality becomes,

1 + mn < m + n

1 + mn - m - n < 0

1 - m + mn - n < 0

(1-m) + n(m-1) < 0

(1-m)(1-n) < 0

(m - 1)(n - 1) < 0

Let us try to plot the graph.

If we consider only mn < 0, then we get 

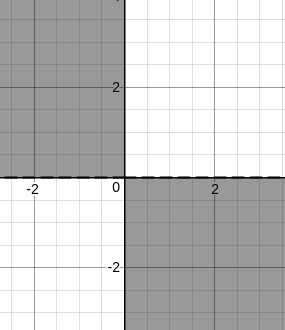
But, we have (m - 1)(n - 1) < 0, so we need to shift the graphs by one unit towards positive x and positive y.

So, we have,

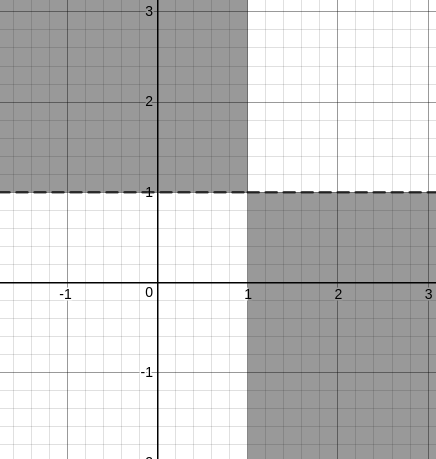
But, we are only considering the first quadrant and the +X and +Y axes. Hence, if we extend, we get the following region.

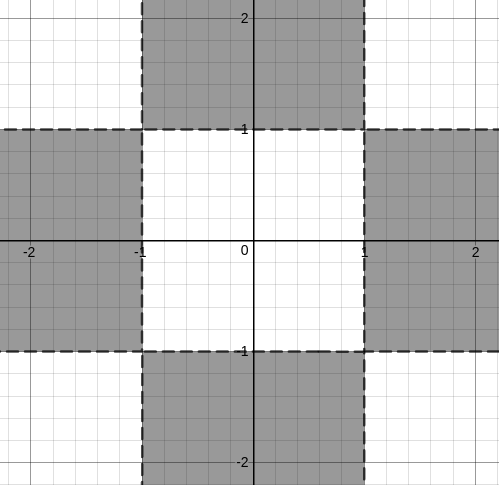
So, if we look for only integer values, we get

(0,2), (0,3),.......

(0,-2), (0, -3),......

(2,0), (3,0), ......

(-2,0), (-3,0), .......

Now, let us consider the other inequation as well, in which |x + y| < 5

Since one of the values is always zero, the modulus of the other value is less than or equal to 4.

Hence, we get 

(0,2), (0,3), (0,4)

(0,-2), (0, -3), (0, -4)

(2,0), (3,0), (4,0)

(-2,0), (-3,0), (-4,0)

Hence, a total of 12 values.